题目内容
17.下面说法中不正确的命题个数为是( )?①命题“?x∈R,x2-x+1≤0”的否定是“$?{x_0}∈R,{x_0}^2-{x_0}+1>0$”;
?②若“p∨q”为假命题,则p,q均为假命题;
?③“mn>0”是“方程mx2+ny2=1表示椭圆”的充分不必要条件.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由全称命题的否定为特称命题,即可判断①;
由复合命题的真值表,即可判断②;
由方程mx2+ny2=1表示椭圆?m>0,n>0且m≠n,即可判断③.
解答 解:对于①,命题“?x∈R,x2-x+1≤0”的否定是“$?{x_0}∈R,{x_0}^2-{x_0}+1>0$”,正确;
对于②,若“p∨q”为假命题,则p,q均为假命题,正确;
对于③,方程mx2+ny2=1表示椭圆?m>0,n>0且m≠n,
则“mn>0”是“方程mx2+ny2=1表示椭圆”的必要不充分条件,故③错.
则不正确的命题个数为1.
故选:B.
点评 本题考查命题的真假判断,主要是命题的否定、复合命题的真假判断以及充分必要条件的判断,考查判断能力,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
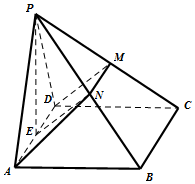 在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.
在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.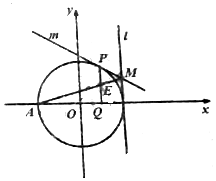 如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.
如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.