题目内容
20．已知tanα=2，则tan（α-$\frac{π}{4}$）=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | -3 |
分析 由题意直接利用两角差的正切公式，求得要求式子的值．
解答 解：∵tanα=2，则tan（α-$\frac{π}{4}$）=$\frac{tanα-1}{1+tanα}$=$\frac{1}{3}$，
故选：B．
点评 本题主要考查两角差的正切公式的应用，属于基础题．
练习册系列答案
相关题目
10．下列各式正确的是（ ）
| A． | tan（-$\frac{13}{4}$π）＜tan（-$\frac{17}{5}$π） | B． | tan（-$\frac{13}{4}$π）＞tan（-$\frac{17}{5}$π） | ||
| C． | tan（-$\frac{13}{4}$π）=tan（-$\frac{17}{5}$π） | D． | 大小关系不确定 |
11．设集合M={x|x2-2x-3≥0}，N={x|-3＜x＜3}，则（ ）
| A． | M⊆N | B． | N⊆M | C． | M∪N=R | D． | M∩N=∅ |
8．已知直线l1：（k+1）x+y+1=0和l2：（k-3）x-ky-1=0，若l1与l2有公共点，则k的取值范围为（ ）
| A． | k≠1且k≠-3 | B． | k≠-3 | C． | k=1 | D． | k=1且k=-3 |
15．要得到函数y=2cos（5x+$\frac{π}{2}$）的图象，只要把函数y=2cos5x的图象上所有的点（ ）
| A． | 向左平移$\frac{π}{10}$个单位长度 | B． | 向右平移$\frac{π}{10}$个单位长度 | ||
| C． | 向左平移$\frac{π}{2}$个单位长度 | D． | 向右平移$\frac{π}{2}$个单位长度 |
12．
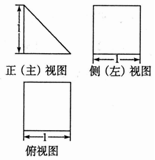某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
9．在正方体ABCD-A1B1C1D1中，直线BB1与平面ACD1所成角的余弦值为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{2}}{3}$ |