题目内容
已知数列|an|满足a1+a2+a3+…+an=2n2-3n,则a5=( )
| A、9 | B、12 | C、15 | D、18 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:利用递推式可得an即可得出.
解答:
解:∵数列|an|满足a1+a2+a3+…+an=2n2-3n,
∴当n≥2时,a1+a2+a3+…+an-1=2(n-1)2-3(n-1),
∴an=4n-5,
∴a5=15.
故选:C.
∴当n≥2时,a1+a2+a3+…+an-1=2(n-1)2-3(n-1),
∴an=4n-5,
∴a5=15.
故选:C.
点评:本题考查了递推式的应用,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
如图是一个四棱锥在空间直角坐标系xoz、xoy、yoz三个平面上的正投影,则此四棱锥的体积为( )
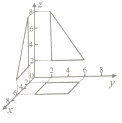

| A、94 | B、32 | C、64 | D、16 |
抛物线C1:x2=2y的焦点为F,以F为圆心C2交C1于A,B两点,交C1准线于C,D两点,若四边形ABCD是矩形,则C2的标准方程为( )
A、x2+(y-
| ||
B、(x-
| ||
C、x2+(y-
| ||
D、(x-
|
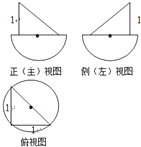 有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).
有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).