题目内容
11.已知公差不为零的等差数列{an},若a1=1,且a1,a2,a5成等比数列.(1)求数列{an}的通项公式;
(2)设bn=2n,求数列{bn-an}的前n项和Sn.
分析 (1)通过a2=1+d、a5=1+4d,利用a1,a2,a5成等比数列计算可知公差d=2,进而可得结论;
(2)分别利用等差数列、等比数列的求和公式计算,相加即可.
解答 解:(1)依题意可知,a2=1+d,a5=1+4d,
∵a1,a2,a5成等比数列,
∴(1+d)2=1+4d,即d2=2d,
解得:d=2或d=0(舍),
∴an=1+2(n-1)=2n-1;
(2)由(1)可知等差数列{an}的前n项和Pn=$\frac{n(1+2n-1)}{2}$=n2,
∵bn=2n,
∴数列{bn}的前n项和Qn=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2,
∴Sn=2n+1-n2-2.
点评 本题考查数列的通项及前n项和,考查等差数列、等比数列的求和公式,考查分组求和法,注意解题方法的积累,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
1.已知O,N,P在所在△ABC的平面内,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=|{\overrightarrow{OC}}|,\overrightarrow{NA}+\overrightarrow{NB}+\overrightarrow{NC}$=$\overrightarrow 0$,且$\overrightarrow{PA}•\overrightarrow{PB}=\overrightarrow{PB}•\overrightarrow{PC}=\overrightarrow{PA}•\overrightarrow{PC}$,则O,N,P分别是△ABC的( )
| A. | 重心 外心 垂心 | B. | 重心 外心 内心 | ||
| C. | 外心 重心 垂心 | D. | 外心 重心 内心 |
6.已知数列{an}中,a1=1,前n项和为Sn,且点P(an,an+1)在直线y=x+1上,则$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{S_n}$=( )
| A. | $\frac{2n}{n+1}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n}{2(n+1)}$ |
3.某校高三共有三个班,其各班人数如表:
(1)从三个班中选一名学生会主席,有多少种不同的选法?
(2)从(1)班、(2)班男生中或从(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?
| 班级 | 男生数 | 女生数 | 总数 |
| 高三(1) | 30 | 20 | 50 |
| 高三(2) | 30 | 30 | 60 |
| 高三(3) | 35 | 20 | 55 |
(2)从(1)班、(2)班男生中或从(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?
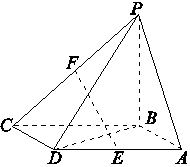 如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.
如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.