题目内容
10.已知抛物线y2=12x,若直线的斜率为k且过点(0,-1),(1)若斜率k=2,求抛物线被直线所截得的弦长;
(2)若直线与抛物线只有一个交点,求斜率k的取值.
分析 (1)设直线与抛物线交于A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}{{y}^{2}=12x}\\{y=2x-1}\end{array}\right.$消y得4x2-16x+1=0,x1+x2=4,${x}_{1}{x}_{2}=\frac{1}{4}$
可得|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=5$\sqrt{3}$
(2)设直线的方程为y-(-1)=kx即y=kx-1
联立$\left\{\begin{array}{l}{{y}^{2}=12x}\\{y=kx-1}\end{array}\right.$消y得k2x2-(2k+12)x+1=0
分k=0,k≠0两种情况讨论
解答 解:(1)设直线与抛物线交于A(x1,y1),B(x2,y2)
由题意得直线的方程为y-(-1)=2(x-0)即y=2x-1
联立$\left\{\begin{array}{l}{{y}^{2}=12x}\\{y=2x-1}\end{array}\right.$消y得4x2-16x+1=0,
x1+x2=4,${x}_{1}{x}_{2}=\frac{1}{4}$
可得|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=5$\sqrt{3}$;
(2)设直线的方程为y-(-1)=kx即y=kx-1
联立$\left\{\begin{array}{l}{{y}^{2}=12x}\\{y=kx-1}\end{array}\right.$消y得k2x2-(2k+12)x+1=0
当k=0时直线y=1与抛物线交于一点($\frac{1}{12}$,0);
当k≠0时,则△=(2k+12)2-4k2=0.
即k=-3,直线y=3x+1与抛物线相切,只有一个交点
综上所述:斜率k为0或-3时,直线与抛物线只有一个交点.
点评 本题考查抛物线与直线的位置关系,方程思想,属于中档题.

| A. | 重心 外心 垂心 | B. | 重心 外心 内心 | ||
| C. | 外心 重心 垂心 | D. | 外心 重心 内心 |
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
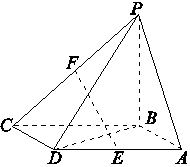 如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.
如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.