题目内容
已知圆O:x2+y2=4和点M(1,a).
(1)若过点M有且只有一条直线与圆O相切,求实数a的值,并求出切线方程;
(2)若a=
,求过点M的最短弦AC与最长弦BD所在的直线方程.并求此时的SABCD.
(1)若过点M有且只有一条直线与圆O相切,求实数a的值,并求出切线方程;
(2)若a=
| 2 |
考点:圆的切线方程,直线与圆的位置关系
专题:计算题,直线与圆
分析:(1)要求过点M的切线方程,关键是求出切点坐标,由M点也在圆上,故满足圆的方程,则易求M点坐标,然后代入圆的切线方程,整理即可得到答案.
(2)当a=
时,M(1,
)在圆x2+y2=4内,由于圆内弦最长的即是圆的直径即BD为直径,而AC是过M且与BD垂直的弦,此时DB=4,圆心(0,0)到直线AC的距离d=
,从而可得,AC=2,即可求出此时的SABCD.
(2)当a=
| 2 |
| 2 |
| 3 |
解答:
解:(1)由条件知点M在圆O上,
∴1+a2=4
∴a=±
当a=
时,点M为(1,
),kOM=
,
此时切线方程为:y-
=-
(x-1)
即:x+
y-4=0;
当a=-
时,点M为(1,-
),kOM=-
,
此时切线方程为:y+
=-
(x-1)
即:x-
y-4=0
∴所求的切线方程为:x+
y-4=0或即:x-
y-4=0
(2)当a=
时,M(1,
)在圆x2+y2=4内,由于圆内弦最长的即是圆的直径即BD为直径,而AC是过M且与BD垂直的弦
此时DB=4,圆心(0,0)到直线AC的距离d=
,
从而可得,AC=2,∴S=
×2×4=4.
∴1+a2=4
∴a=±
| 3 |
当a=
| 3 |
| 3 |
| 3 |
此时切线方程为:y-
| 3 |
| ||
| 3 |
即:x+
| 3 |
当a=-
| 3 |
| 3 |
| 3 |
此时切线方程为:y+
| 3 |
| ||
| 3 |
即:x-
| 3 |
∴所求的切线方程为:x+
| 3 |
| 3 |
(2)当a=
| 2 |
| 2 |
此时DB=4,圆心(0,0)到直线AC的距离d=
| 3 |
从而可得,AC=2,∴S=
| 1 |
| 2 |
点评:本题考查的是圆的切线方程,即直线与圆方程的应用.(求过一定点的圆的切线方程,首先必须判断这点是否在圆上.若在圆上,则该点为切点,若点P(x0,y0)在圆(x-a)2+(y-b)2=r2(r>0)上,则 过点P的切线方程为(x-a)(x0-a)+(y-b)(y0-b)=r2(r>0);若在圆外,切线应有两条.一般用“圆心到切线的距离等于半径长”来解较为简单.若求出的斜率只有一个,应找出过这一点与x轴垂直的另一条切线.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
若a>1,则函数y=(
)•ax的图象的基本形状是( )
| x |
| |x| |
A、 |
B、 |
C、 |
D、 |
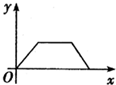 如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )
如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )