题目内容
11.若圆x2+(y-1)2=r2与曲线(x-1)y=1没有公共点,则半径r的取值范围是( )| A. | 0<r<$\sqrt{2}$ | B. | 0<r<$\frac{\sqrt{11}}{2}$ | C. | 0<r<$\sqrt{3}$ | D. | 0<r<$\frac{\sqrt{13}}{2}$ |
分析 求得圆的圆心和半径,设圆与曲线y=$\frac{1}{x-1}$相切的切点为(m,n),代入曲线的方程,求出函数的导数和切线的斜率,由两点的斜率公式和两直线垂直的条件:斜率之积为-1,解方程可得切点,进而得到此时圆的半径,结合图象即可得到所求范围.
解答 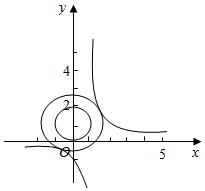 解:圆的圆心为(0,1),半径为r
解:圆的圆心为(0,1),半径为r
设圆与曲线y=$\frac{1}{x-1}$相切的切点为(m,n),
可得n=$\frac{1}{m-1}$,①
y=$\frac{1}{x-1}$的导数为y′=-$\frac{1}{(x-1)^{2}}$,
可得切线的斜率为-$\frac{1}{(m-1)^{2}}$,
由两点的斜率公式可得$\frac{n-1}{m-0}$•(-$\frac{1}{(m-1)^{2}}$)=-1,
即为n-1=m(m-1)2,②
由①②可得n4-n3-n-1=0
化为(n2-n-1)(n2+1)=0,
即有n2-n-1=0,解得n=$\frac{\sqrt{5}+1}{2}$或$\frac{1-\sqrt{5}}{2}$,
则有$\left\{\begin{array}{l}{m=\frac{1+\sqrt{5}}{2}}\\{n=\frac{1+\sqrt{5}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{1-\sqrt{5}}{2}}\\{n=\frac{1-\sqrt{5}}{2}}\end{array}\right.$.
可得此时圆的半径r=$\sqrt{{m}^{2}+(n-1)^{2}}$=$\sqrt{3}$.
结合图象即可得到圆与曲线没有公共点的时候,
r的范围是(0,$\sqrt{3}$).
另解:设双曲线与y轴交于B,延长BO'交双曲线于C,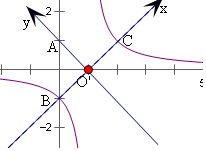
O'A=O'B=$\sqrt{2}$,BC⊥AO',
建立直角坐标系xO'y,双曲线的方程为x2-y2=2,
由AO'=$\sqrt{2}$,A在新坐标系下的坐标为(0,$\sqrt{2}$),
圆A方程变为x2+(y-$\sqrt{2}$)2=r2,
x2=y2+2,代入圆方程可得y2+2+y2-2$\sqrt{2}$y+2-r2=0,
运用△=8-4×2×(4-r2)<0,
解得-$\sqrt{3}$<r<$\sqrt{3}$,
由r>0,可得r的范围是(0,$\sqrt{3}$).
故选:C.
点评 本题考查圆与曲线的位置关系的判断,注意运用导数求得切线的斜率,考查化简整理的运算能力,属于中档题.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | -$\frac{4}{9}$$\sqrt{2}$ | B. | $\frac{4}{9}$$\sqrt{2}$ | C. | ±$\frac{4}{9}$$\sqrt{2}$ | D. | -$\frac{7}{9}$ |
| A. | (1007$\sqrt{2}$,1007$\sqrt{2}$) | B. | (-1007$\sqrt{2}$,1007$\sqrt{2}$) | C. | (1007,1007$\sqrt{3}$) | D. | (1007$\sqrt{3}$,1007) |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
(1)求b;
(2)有评估机构从以往购买了车险的车辆中随机抽取了1000辆调查,得到一年中出险次数的频数分布如下(并用相应频率估计2016年度出险次数的概率):
| 一年中出险的次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 频数 | 500 | 380 | 100 | 15 | 4 | 1 |
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 1.2 | B. | -1.2 | C. | -2.3 | D. | 7.5 |
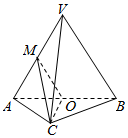 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.