题目内容
19．已知如下等式：2+4=6；
8+10+12=14+16；
18=20+22+24=26+28+30；
…
以此类推，则2018出现在第31个等式中．
分析 从已知等式分析，发现规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，即可得出结论．
解答 解：①2+4=6；
②8+10+12=14+16；
③18+20+22+24=26+28+30，…
其规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，
所以第n个等式的首项为2[1+3+…+（2n-1）]=2×$\frac{n（1+2n-1）}{2}$=2n2，
当n=31时，等式的首项为2×312=1932，
当n=32时，等式的首项为2×322=2048，
所以2018在第31个等式中，
故答案为：31
点评 本题考查归纳推理，难点是根据能够找出数之间的内在规律，考查观察、分析、归纳的能力，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
9．函数y=sin（ωx+θ-$\frac{π}{6}$）的最小正周期为π，且其图象向左平移$\frac{π}{6}$单位得到的函数为奇函数，则θ的一个可能值是（ ）
| A． | $\frac{π}{3}$ | B． | -$\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | -$\frac{π}{6}$ |
10．二项式${（{\sqrt{x}-\frac{1}{{\sqrt{x}}}}）^{12}}$展开式中，x3的系数是（ ）
| A． | -495 | B． | -220 | C． | 495 | D． | 220 |
14．已知函数f（x）=（2x-x2）ex，给以下四个结论：①f（x）＞0的解集为{x|0＜x＜2}；②$f（{-\sqrt{2}}）$是极小值，$f（{\sqrt{2}}）$是极大值；③f（x）有极小值，但无最小值；④f（x）有极小值，也有最小值．其中正确的是（ ）
| A． | ①② | B． | ①②③ | C． | ①②④ | D． | ②④ |
11．若数列{an}满足a1=1，an+1=nan+1，则第5项a5=（ ）
| A． | 5 | B． | 65 | C． | 89 | D． | 206 |
9．
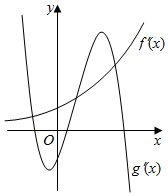定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（ ）
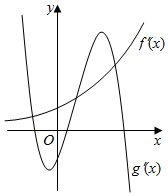定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（ ）| A． | 只有三个极大值点，无极小值点 | B． | 有两个极大值点，一个极小值点 | ||
| C． | 有一个极大值点，两个极小值点 | D． | 无极大值点，只有三个极小值点 |