题目内容
10.二项式${({\sqrt{x}-\frac{1}{{\sqrt{x}}}})^{12}}$展开式中,x3的系数是( )| A. | -495 | B. | -220 | C. | 495 | D. | 220 |
分析 利用二项式定理的通项公式即可得出.
解答 解:通项公式:Tr+1=${∁}_{12}^{r}$$(\sqrt{x})^{12-r}$$(-\frac{1}{\sqrt{x}})^{r}$=(-1)r${∁}_{12}^{r}$x6-r,令6-r=3,解得r=3.
∴x3的系数=-${∁}_{12}^{3}$=-220.
故选:B.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.已知变量x和y的统计数据如表:
根据该表可得回归直线方程$\widehat{y}$=0.7x+a,据此可以预测当x=15时,y=( )
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 7.8 | B. | 8.2 | C. | 9.6 | D. | 8.5 |
18.在平面直角坐标系xOy中,已知成$\overrightarrow{OA}$=(-1,t),$\overrightarrow{OB}$=(2,2),若∠ABO=90°,则实数t的值为( )
| A. | 1 | B. | -3 | C. | $\frac{1}{3}$ | D. | 5 |
5.两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2017项为a2017,则a2017-5=( )


| A. | 2023×2017 | B. | 2023×2016 | C. | 1008×2023 | D. | 2017×1008 |
20.已知函数f(x)=sin(ωx+φ)+1(ω>0,0≤φ≤$\frac{π}{2}$)的图象相邻两条对称轴之间的距离为π,且在x=$\frac{π}{3}$时取得最大值2,若f(α)=$\frac{8}{5}$,且$\frac{π}{3}$<α<$\frac{5π}{6}$,则sin(2α+$\frac{π}{3}$)的值为( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
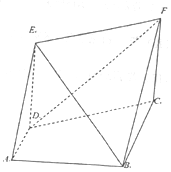 如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.
如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.