题目内容
9.函数y=sin(ωx+θ-$\frac{π}{6}$)的最小正周期为π,且其图象向左平移$\frac{π}{6}$单位得到的函数为奇函数,则θ的一个可能值是( )| A. | $\frac{π}{3}$ | B. | -$\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | -$\frac{π}{6}$ |
分析 根据函数的周期算出ω=2,从而得到函数表达式为sin(2x+θ-$\frac{π}{6}$)所以得出函数图象向左平移$\frac{π}{6}$个单位后,得到y=sin(2x+θ+$\frac{π}{6}$)的图象,再根据奇函数的特性取x=0,得sin(θ+$\frac{π}{6}$)=0,可得θ=kπ-$\frac{π}{6}$,(k∈Z),即可得到答案.
解答 解:∵y=sin(ωx+θ-$\frac{π}{6}$)的最小正周期为π,
∴ω=$\frac{2π}{T}$=2,得函数表达式为f(x)=sin(2x+θ-$\frac{π}{6}$)
将函数的图象向左平移$\frac{π}{6}$个单位后,
得到的函数为y=f(x+$\frac{π}{6}$)=sin[2(x+$\frac{π}{6}$)+θ-$\frac{π}{6}$]=sin(2x+θ+$\frac{π}{6}$)
由题意,得函数为y=sin(2x+θ+$\frac{π}{6}$)为奇函数,
∴f(0)=sin(θ+$\frac{π}{6}$)=0,
解之得θ+$\frac{π}{6}$=kπ,所以θ=kπ-$\frac{π}{6}$,(k∈Z),
∴取k=0,得θ=-$\frac{π}{6}$
故选:D
点评 本题给出一个三角函数式,将其图象平移得到奇函数的图象,求初相φ的值,着重考查了函数y=Asin(ωx+φ)的图象与性质等知识,属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
4.将函数$y=sin(x+\frac{π}{6})$的图象向左平移π个单位,则平移后的函数图象( )
| A. | 关于直线$x=\frac{π}{3}$对称 | B. | 关于直线$x=\frac{π}{6}$对称 | ||
| C. | 关于点$(\frac{π}{3},0)$对称 | D. | 关于点$(\frac{π}{6},0)$对称 |
1.已知变量x和y的统计数据如表:
根据该表可得回归直线方程$\widehat{y}$=0.7x+a,据此可以预测当x=15时,y=( )
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 7.8 | B. | 8.2 | C. | 9.6 | D. | 8.5 |
18.在平面直角坐标系xOy中,已知成$\overrightarrow{OA}$=(-1,t),$\overrightarrow{OB}$=(2,2),若∠ABO=90°,则实数t的值为( )
| A. | 1 | B. | -3 | C. | $\frac{1}{3}$ | D. | 5 |
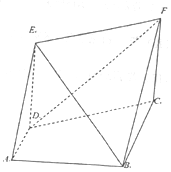 如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.
如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.