题目内容
设f（x）=cos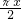
，x∈z，则f（25）+f（26）+f（27）+…+f（46）=________．
-1
分析：先求出函数f（x）=cos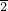
，x∈z的周期等于4，计算函数在一个周期内的函数值的和，即可得到要求的式子的值．
解答：由于函数f（x）=cos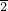，x∈z的周期等于4，
∵f（25）+f（26）+f（27）+f（28）=0-1+0+1=0，
∴f（25）+f（26）+f（27）+…+f（46）=0+f（45）+f（46）=0-1=-1．
故答案为：-1．
点评：本题主要考查三角函数的周期性及其求法，利用诱导公式和三角函数的周期性求出三角函数的值，判断要求式子的值等于
f（45）+f（46），是解题的关键．
分析：先求出函数f（x）=cos
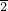，x∈z的周期等于4，计算函数在一个周期内的函数值的和，即可得到要求的式子的值．解答：由于函数f（x）=cos
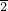，x∈z的周期等于4，∵f（25）+f（26）+f（27）+f（28）=0-1+0+1=0，
∴f（25）+f（26）+f（27）+…+f（46）=0+f（45）+f（46）=0-1=-1．
故答案为：-1．
点评：本题主要考查三角函数的周期性及其求法，利用诱导公式和三角函数的周期性求出三角函数的值，判断要求式子的值等于
f（45）+f（46），是解题的关键．
练习册系列答案
相关题目
设f（x）=cos（x+θ）+
sin（x+φ）是偶函数，其中θ，φ均为锐角，且cosθ=
sinφ，则θ+φ=（ ）
| 2 |
| ||
| 3 |
A、
| ||
| B、π | ||
C、
| ||
D、
|