题目内容
求函数y=5
-
的值域．
| x2+2x+3 |
| x2+4x+5 |
考点：函数的值域
专题：函数的性质及应用
分析：通过对函数求导找到函数的单调区间，确定最小值，从而确定函数的值域．
解答：
解：y′=5•
(x2+2x+3)-
•（x2+2x+1）′-
(x2+4x+5)-
•（x2+4x+5）′
=
-
，
令y′=0，
∴
=0
∴解得：x=-
．
∴在（-∞，-
）上y单调递减，在（-
，+∞）单调递增，
∴当x=-
时，y最小，y最小=
，
∴函数y的值域为：[
，+∞）．
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 5(x+1) | ||
|
| x+2 | ||
|
令y′=0，
∴
5(x+1)
| ||||
|
∴解得：x=-
| 3 |
| 4 |
∴在（-∞，-
| 3 |
| 4 |
| 3 |
| 4 |
∴当x=-
| 3 |
| 4 |
5
| ||||
| 4 |
∴函数y的值域为：[
5
| ||||
| 4 |
点评：本题考察了函数的值域问题，通过求导是求函数值域的方法之一，本题是一道基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
若曲线y=x3在点P处的切线斜率为k=3，则点P的坐标为（ ）
| A、（1，1） |
| B、（-1，-1） |
| C、（1，1），（-1，-1） |
| D、（2，8），（-2，-8） |
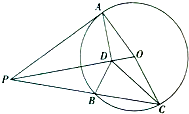如图，AP是圆O的切线，A是切点，AD⊥OP与D点，过点P作圆O的割线与圆O相交于B，C两点