题目内容
已知函数f（x）=2cos2x+
sin2x，x∈R．
（1）求f（x）的最小正周期及最大值；
（2）求f（x）的单调递增区间．
| 3 |
（1）求f（x）的最小正周期及最大值；
（2）求f（x）的单调递增区间．
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）利用二倍角公式和两角和公式对函数解析式化简，进而根据周期公式求得函数的最小正周期，根据正弦函数的性质求得函数的最大值．
（2）利用整体法根据正弦函数的单调性求得函数的单调递增区间．
（2）利用整体法根据正弦函数的单调性求得函数的单调递增区间．
解答：
解：（1）f（x）=cos2x+1+
sin2x=2sin（2x+
）+1，
∴T=
=π，f（x）max=2+1=3．
（2）由2kπ-
≤2x+
≤2kπ+
，求得kπ-
≤x≤kπ+
，k∈Z，
∴函数的单调递增区间为[得kπ-
，kπ+
]（k∈Z）．
| 3 |
| π |
| 6 |
∴T=
| 2π |
| 2 |
（2）由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数的单调递增区间为[得kπ-
| π |
| 3 |
| π |
| 6 |
点评：本题主要考查了三角函数恒等变换的应用，三角函数图象与性质．解题时可注意与正弦函数图象相结合来解决．
练习册系列答案
相关题目
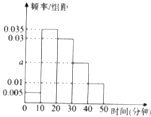经统计，某校学生上学路程所需要时间全部介于0与50之间（单位：分钟），现从在校学生中随机抽取100人，按上学所需时间分组如下：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到如图所示的频率分布直方图．
