题目内容

lg2+lg50=（　　）
A、1B、2C、3D、4
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算法则即可得出．
解答： 解：原式=lg（2×50）=lg102=2．
故选：B．
点评：本题考查了对数的运算法则，属于基础题．
练习册系列答案
相关题目
四棱锥的三视图如图所示，则此四棱锥的内切球半径为
 
．
下列各组中表示同一函数的是（　　）
A、f（x）=x-1，g（x）=
x2
x
-1
B、f（x）=x2，g（x）=
3x6
C、f（x）=1，g（x）=x0
D、f（x）=x2，g（x）=（
x 
）4
如果f（x）=mx2+（m-1）x+1在区间（-∞，1]上为减函数，则m的取值范围（　　）
A、（0，
1
3
]
B、[0，
1
3
）
C、[0，
1
3
]
D、（0，
1
3
）
计算3log34+2 4+log25=（　　）
A、80B、84C、16D、32
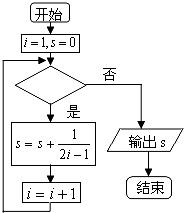如图给出的是计算1+
1
3
+
1
5
+…+
1
2013
的值的一个程序框图，则判断框内应填人的条件是（　　）
A、i≤1006
B、i＞1006
C、i≤1007
D、i＞1007
图为一个半球挖去一个圆锥的几何体的三视图，则该几何体的表面积为（　　）
A、（
8
3
+2
2
）π
B、（
8
3
+4
2
）π
C、（4+2
2
）π
D、（8+4
2
）π
若f（cosx）=
x
2
，x∈[0，π]，则f（-
1
2
）等于（　　）
A、cos
1
2
B、
π
3
C、
π
4
D、
2π
3
已知函数f（x）=ax+xlnx的图象在点x=e（e为自然对数的底数）处的切线斜率为3．
（1）求实数a的值；
（2）若k∈Z，不等式k（x-1）＜f（x）在x∈（1，+∞）上恒成立，求k的最大值；
（3）当n＞m≥4时，证明：（mnn）m＞（nmm）n．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网