题目内容
6.已知函数f(x)=$\frac{ln(1+x)}{x}$.(1)试判断函数f(x)在(0,+∞)上的单调性,并说明理由;
(2)若函数f(x)在其定义域内恒有f(x)<$\frac{1-ax}{1+x}$成立,试求a的所有可能的取值的集合.
分析 (1)已知f(x),构造新的函数g(x),利用导数求函数单调的方法步骤;
(2)由f(x)<$\frac{1-ax}{1+x}$得$\frac{(1+x)ln(1+x)-x+{ax}^{2}}{x}$<0,令h(x)=(1+x)ln(1+x)-x+ax2,显然h(0)=0,求出函数的导数,令g(x)=ln(1+x)+2ax,通过讨论a的范围判断即可.
解答 解:(1)∵f(x)=$\frac{ln(1+x)}{x}$,(x>0)
∴f′(x)=$\frac{\frac{x}{1+x}-ln(1+x)}{{x}^{2}}$,
设g(x)=$\frac{x}{1+x}$-ln(1+x),(x≥0).
∴g′(x)=$\frac{1-(1+x)}{{(1+x)}^{2}}$=$\frac{-x}{{(1+x)}^{2}}$≤0,
∴y=g(x)在[0,+∞)上为减函数.
∴g(x)=$\frac{x}{1-x}$-ln(1+x)≤g(0)=0,
∴f′(x)<0,
∴函数f(x)在(0,+∞)上为减函数.
(2)f(x)的定义域是(-1,0)∪(0,+∞),
由f(x)<$\frac{1-ax}{1+x}$得$\frac{(1+x)ln(1+x)-x+{ax}^{2}}{x}$<0,
令h(x)=(1+x)ln(1+x)-x+ax2,显然h(0)=0,
则h′(x)=ln(1+x)+2ax,令g(x)=ln(1+x)+2ax,
g′(x)=$\frac{1}{1+x}$+2a,h′(0)=0,
①2a<-1时,即a<-$\frac{1}{2}$,
令g′(x)<0,有h′(x)在(-1-$\frac{1}{2a}$,0)递减,
h′(x)>h′(0)=0,故h(x)在(-1-$\frac{1}{2a}$,0)递增,
故h(x)<h(0)=0,$\frac{h(x)}{x}$>0,
此时f(x)>$\frac{1-ax}{1+x}$不合题意;
②2a=-1即a=-$\frac{1}{2}$时,g′(x)=-$\frac{x}{x+1}$,令g′(x)>0,
故h′(x)在(-1,0)递增,h′(x)<h′(0)=0,
h(x)在(-1,0)递减,故h(x)>h(0)=0,即$\frac{h(x)}{x}$<0;
令g′(x)<0,即h′(x)在(0,+∞)递减,
h′(x)<h′(0)=0,
故h(x)在(0,+∞)递减,
故h(x)<h(0)=0,即$\frac{h(x)}{x}$<0,
故对于x∈(-1,0)∪(0,+∞)有$\frac{(1+x)ln(1+x)-x+{ax}^{2}}{x}$<0成立,
即f(x)<$\frac{1-ax}{1+x}$,
③-1<2a<0即-$\frac{1}{2}$<a<0时,令g′(x)>0,
故任意x∈(0,-1-$\frac{1}{2a}$),g′(x)>0,h′(x)在(0,-1-$\frac{1}{2a}$)递增,
h′(x)>h′(0)=0,故h(x)在(0,-1-$\frac{1}{2a}$)是增函数,
故h(x)>h(0)=0,即$\frac{h(x)}{x}$>0,此时f(x)>$\frac{1-ax}{1+x}$,不合题意;
④a≥0时,令g′(x)>0,得h′(x)在(0,+∞)递增,
h′(x)>h′(0)=0,
故h(x)在(0,+∞)递增,故h(x)>h(0)=0,即$\frac{h(x)}{x}$>0,
此时f(x)>$\frac{1-ax}{1+x}$,不合题意,
综上,a=-$\frac{1}{2}$时,对于任意x∈(-1,0)∪(0,+∞)时,f(x)<$\frac{1-ax}{1+x}$.
点评 本题综合性较强,主要考查利用导数研究函数的单调性,以此为主线,贯穿其中.但对以上问题的解答,关键是构造函数,这是函数这一章节的重点和难点.

| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{8}{3}$ |
| A. | $\frac{\sqrt{5}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
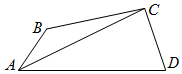 如图,在四边形ABCD中,AB=5,BC=7,AC=8,CD=6,BC⊥CD.
如图,在四边形ABCD中,AB=5,BC=7,AC=8,CD=6,BC⊥CD.