Question

14．某市大型国有企业按照中央“调结构、保增长、促发展”的指示精神，计划投资甲乙两个项目，前期调研获悉，甲项目每投资百万元需要配套电能2万千瓦，增加产值200万元；乙项目每投资百万元需要配套电能4万千瓦，增加产值300万元，根据该企业目前资金储备状况仅能最多投资3000万元，配套电能100万千瓦．
（Ⅰ）假设企业在甲、乙两个项目投资额分别为x，y（单位：百万元），请写出x，y所满足的约束条件，并在所给出的坐标系画出可行域；
（Ⅱ）计算如何安排对甲、乙两个项目投资额，才能使产值有最大的增加值．

Answer 1

分析 （I）由题意知投资额x，y所满足的约束条件$\left\{\begin{array}{l}x+y≤30\\ 2x+4y≤100\\ x≥0，y≥0\end{array}\right.$，分别求出O，A，B，C四点的坐标，画出不等式组表示的可行域；
（II）目标函数为z=200x+300y，可通过z=0的直线平移可得经过A点时取得最大值．

解答 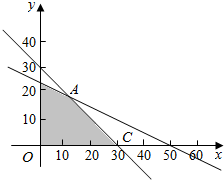解：（I）由题意知投资额x，y所满足的约束条件为
$\left\{\begin{array}{l}x+y≤30\\ 2x+4y≤100\\ x≥0，y≥0\end{array}\right.$，
对应的边界点分别为O（0，0），A（10，20），
B（0，25），C（30，0），
如图，可行域为四边形OCAB及其内部区域（含边界）．
（II）目标函数为z=200x+300y，其斜率为$k=-\frac{2}{3}$，
而可行域的边界对应的斜率分别为$-1，-\frac{1}{2}$，
所以当目标函数对应的动直线z=200x+300y经过点A（10，20）时，
即甲、乙两个项目投资额分别安排1000万元、2000万元，才能使产值有最大的增加值．

点评 本题考查简单线性规划的运用，考查数形结合的思想方法，以及运算能力，属于中档题．