题目内容
如图,将一个边长为1的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)…
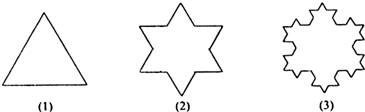
则前n个图形的边数的总和为 .

则前n个图形的边数的总和为
考点:归纳推理
专题:等差数列与等比数列,推理和证明
分析:记第n个图形的边数为an,根据图形得到,a1=3,a2=12,a3=48,由题意知:每一条边经一次变化后总变成四条边,即
=4,由等比数列的定义,可求第n个图形的边数an,进而得到前n个图形的边数的总和
| an | ||
|
解答:
解:∵a1=3,a2=12,a3=48,由题意知:每一条边经一次变化后总变成四条边,即
=4,
由等比数列的定义知:an=3×4n-1
故前n个图形的边数的总和为:
=4n-1,
故答案为:4n-1
| an | ||
|
由等比数列的定义知:an=3×4n-1
故前n个图形的边数的总和为:
| 3(1-4n) |
| 1-4 |
故答案为:4n-1
点评:本题的肯定是数列的应用,主要考查对图形的阅读能力,考查数列模型的建立,考查等比数列的通项公式和前n项和公式.

练习册系列答案
相关题目
将函数y=sin(2x-
)的图象向右平移
个单位,得到的图象的解析式是( )
| π |
| 6 |
| π |
| 3 |
| A、A、y=cos2x | ||
B、y=sin(2x+
| ||
C、y=sin(2x-
| ||
D、y=sin(2x-
|
已知数列{an}中,a1=2,an+1=an+
(n∈N*),则a99的值为( )
| 1 |
| 2 |
| A、48 | B、49 | C、50 | D、51 |
已知角α终边上一点的坐标为(4,-3),则cosα=( )
A、-
| ||
B、
| ||
C、-
| ||
D、-
|
 以等腰△ABC的斜边AB上的高CD为棱折成一个60°的二面角,使B到B′的位置,已知斜边AB=2,则顶点A到平面CB′D的距离是
以等腰△ABC的斜边AB上的高CD为棱折成一个60°的二面角,使B到B′的位置,已知斜边AB=2,则顶点A到平面CB′D的距离是