题目内容
函数f(x)=|sinx|+2|cosx|的值域为( )
| A、[1,2] | ||
B、[
| ||
C、[2,
| ||
D、[1,
|
考点:三角函数值的符号,函数的值域
专题:三角函数的图像与性质
分析:先将函数y=|sinx|+2|cosx|的值域?当x∈[0,
]时,y=sinx+2cosx的值域,利用两角和与差的正弦函数化简,由正弦函数的性质求出函数的值域.
| π |
| 2 |
解答:
解:∵函数y=|sinx|+2|cosx|的值域?当x∈[0,
]时,y=sinx+2cosx的值域,
∴y=sinx+2cosx=
sin(x+θ)(其中θ是锐角,sinθ=
、cosθ=
),
由x∈[0,
]得,x+θ∈[θ,
+θ],
所以cosθ≤sin(x+θ)≤1,即
≤sin(x+θ)≤1,
所以1≤
sin(x+θ)≤
,
则函数y=|sinx|+2|cosx|的值域是[1,
],
故选:D.
| π |
| 2 |
∴y=sinx+2cosx=
| 5 |
2
| ||
| 5 |
| ||
| 5 |
由x∈[0,
| π |
| 2 |
| π |
| 2 |
所以cosθ≤sin(x+θ)≤1,即
| ||
| 5 |
所以1≤
| 5 |
| 5 |
则函数y=|sinx|+2|cosx|的值域是[1,
| 5 |
故选:D.
点评:本题考查两角和与差的正弦函数,正弦函数的性质,将函数y=|sinx|+2|cosx|的值域?当x∈[0,
]时,y=sinx+2cosx的值域,是解题的关键,考查等价转化思想与运算求解能力,属于中档题.
| π |
| 2 |

练习册系列答案
相关题目
某种树的分枝生长规律如图所示,则预计到第6年树的分枝数为( )


| A、5 | B、6 | C、7 | D、8 |
已知i是虚数单位,则
=( )
| i |
| 1-i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
“x≠1且y≠2”是“x+y≠3”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
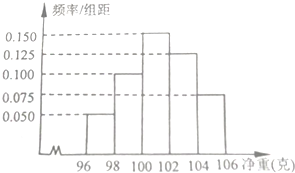 某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104]上的产品件数是
某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104]上的产品件数是