题目内容
已知数列{an}的前n项和为Sn,且a1=1,an+1=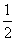 Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)求数列{an}的通项公式;
(2)当bn=log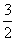 (3an+1)时,求证:数列
(3an+1)时,求证:数列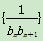 的前n项和Tn=
的前n项和Tn=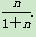
(1)解 由已知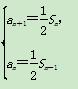 (n≥2),
(n≥2),
得an+1=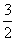 an(n≥2).
an(n≥2).
∴数列{an}是以a2为首项,以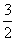 为公比的等比数列.
为公比的等比数列.
又a2=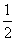 S1=
S1=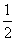 a1=
a1=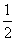 ,
,
∴an=a2×(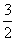 )n-2(n≥2).
)n-2(n≥2).
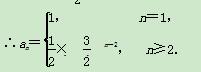
(2)证明 bn=log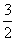 (3an+1)=log
(3an+1)=log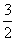 [
[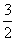 ×(
×(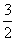 )n-1]=n.
)n-1]=n.
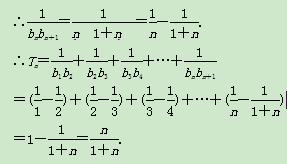

练习册系列答案
相关题目

 )=
)= ,(k=1,2,3), 其中c为常数,则E
,(k=1,2,3), 其中c为常数,则E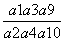 等于( )
等于( )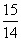 B.
B.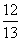 C.
C.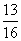 D.
D.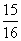
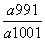 <0.给出下列结论:①0<q<1;②a99a101-1<0;③T100的值是Tn中最大的;④使Tn>1成立的最大自然数n等于198.其中正确的结论是________.(填写所有正确的序号)
<0.给出下列结论:①0<q<1;②a99a101-1<0;③T100的值是Tn中最大的;④使Tn>1成立的最大自然数n等于198.其中正确的结论是________.(填写所有正确的序号) 若目标函数z=ax+by(a>0,b>0)的最大值为12,则
若目标函数z=ax+by(a>0,b>0)的最大值为12,则 +
+ 的最小值为( )
的最小值为( ) B.
B. C.
C. D.4
D.4 ,且a+b+c=1 (其中a,b,c为正实数),则M的取值范围是( )
,且a+b+c=1 (其中a,b,c为正实数),则M的取值范围是( ) C.[1,8) D.[8,+∞)
C.[1,8) D.[8,+∞)