题目内容
19. 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=PA=1,且.PA⊥平面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=PA=1,且.PA⊥平面ABCD.(1)求证:PB⊥AC;
(2)求顶点A到平面PCD的距离.
分析 (I)推导出PA⊥AC,AB⊥AC,由此能证明AC⊥平面PAB,从而PB⊥AC.
(Ⅱ)推导出AC⊥CD,PA⊥CD,从而CD⊥平面PAC,进而平面PCD⊥平面PAC,过A作AH⊥PC,垂足为H,则AH⊥平面PCD,由此能求出A到平面PCD的距离.
解答 (本题满分12分)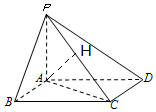
证明:(I)∵PA⊥平面ABCD,AC?平面ABCD,∴PA⊥AC;…(2分)
在△ABC中,∠ABC=60°,BC=2,AB=1,
∴AC2=AB2+BC2-2 AB•BC cos60°=1+4-2=3,则AB2+AC2=BC2,
∴AB⊥AC,…(4分)
又PA∩AB=A,∴AC⊥平面PAB,
∵PB?平面PAB,∴PB⊥AC.…(6分)
解:(Ⅱ)由(I)知:AC⊥CD,又PA⊥CD,则CD⊥平面PAC,
∵CD?平面PCD,∴平面PCD⊥平面PAC;…(8分)
过A作AH⊥PC,垂足为H,则AH⊥平面PCD;…(10分)
在Rt△PAC中,AH=$\frac{PA•AC}{PC}$=$\frac{\sqrt{3}}{2}$.
即A到平面PCD的距离为$\frac{\sqrt{3}}{2}$.…(12分)
点评 本题考查线线垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力,空间想象能力,考查化归与转化思想,是中档题.

练习册系列答案
相关题目
9.设直线x=m分别交函数$y=sinx、y=sin(x+\frac{π}{2})$的图象于M、N、两点,则M、N距离的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
10.已知函数y=f(x)是定义在R上以π为周期的奇函数,且当x∈[-$\frac{π}{2}$,0)时,f(x)=sinx,则f(-$\frac{5π}{3}$)=( )
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
4.执行如图所示的程序框图,若输入m=3,n=4,则输出a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
8.不等式|x-1|<2的解集是( )
| A. | (-∞,-1) | B. | (-∞,1) | C. | (-1,3) | D. | (-∞,-1)∪(3,+∞) |