题目内容
13. (1)由圆x2+y2=4上任意一点向x轴作垂线,求垂线夹在圆周和x轴间的线段中点的轨迹方程;
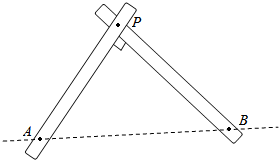
(1)由圆x2+y2=4上任意一点向x轴作垂线,求垂线夹在圆周和x轴间的线段中点的轨迹方程;(2)两根杆分别绕着定点A和B(AB=2a)在平面内转动,并且转动时两杆保持互相垂直,求杆的交点P的轨迹方程.
分析 (1)利用中点坐标公式,确定P,M坐标之间的关系,将P的坐标代入圆的方程,即可求得M的轨迹方程.
(2)根据题意,AB是定值,且两根杆永远垂直,所以我们可以判定P的轨迹为圆 其中AB为直径 两根杆所成的角即为圆周角,以AB为x轴,以AB中点为原点建系,即可得到圆的轨迹方程.
解答 解:(1)设垂线夹在圆周和x轴间的线段中点M(x,y),则P(x,2y)
∵P在圆x2+y2=4上,
∴x2+4y2=4,
∴$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(2)根据题意,AB是定值,且两根杆永远垂直,所以我们可以判定P的轨迹为圆,其中AB为直径 两根杆所成的角即为圆周角
以AB为x轴,以AB中点为原点建系 直径AB=2a,
∴圆的轨迹方程:x2+y2=a2(x≠±a).
点评 本题考查轨迹方程,考查直接法、代入法的运用,考查学生的计算能力,确定坐标之间的关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.直线2x+3y-1=0垂直于向量$\overrightarrow{n}$=(m,-1),则m的值为( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |