题目内容

5．已知集合A={（x，y）|（1-a）x2+2xy-ay2≤0}，B={（x，y）|3x-5y≥0，x，y＞0}，且B⊆A，则实数a的最小值为$\frac{55}{34}$．

分析 由B求出$\frac{x}{y}$的范围，把A化为关于$\frac{x}{y}$的不等式，结合B⊆A，可得关于a的不等式求解．

解答 解：由B={（x，y）|3x-5y≥0，x，y＞0}={（x，y）|$\frac{x}{y}≥\frac{5}{3}$}，
A═{（x，y）|（1-a）x2+2xy-ay2≤0}={（x，y）|$（1-a）\frac{{x}^{2}}{{y}^{2}}+2\frac{x}{y}-a≤0$}，
∵B⊆A，∴$（1-a）×（\frac{5}{3}）^{2}+2×\frac{5}{3}-a≤0$，解得a$≥\frac{55}{34}$．
∴实数a的最小值为$\frac{55}{34}$．
故答案为：$\frac{55}{34}$．

点评 本题考查集合的包含关系的判定与应用，考查了数学转化思想方法，是中档题．

练习册系列答案
相关题目
4．设a=20.3，b=0.22，c=logx（x2+0.3）（x＞1），则a，b，c的大小关系是（　　）
A．a＜b＜cB．b＜a＜cC．c＜b＜aD．b＜c＜a
5．已知A={1，3，9，27，81}，B={y|y=log3x，x∈A}，则A∩B=（　　）
A．{1，3}B．{3，27，81}C．{1，3，9}D．{9，27}
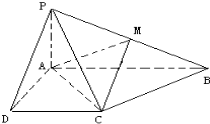2．如图所示，在四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠DAB=90°，PA⊥平面ABCD，且PA=CD=AD=$\frac{1}{2}$AB，M为PB的中点．
（1）证明：平面PAD⊥平面PCD；
（2）求二面角A-MC-B的余弦值．
9．正四棱锥底面边长为a，侧棱长为a，则其表面积为$（\sqrt{3}+1）{a}^{2}$．
10．数列{an}中，${a_n}+{a_{n+2}}=2{a_{n+1}}（{n∈{N^*}}），{a_5}=5$，则有（　　）
A．a4•a6=25B．a4•a6≤25C．a4•a6＞25D．a4•a6＜25
17．已知函数$f（x）=\frac{x}{lnx}-ax$．
（1）a=1，x＞1时，求证：$f（x）•\frac{x-1}{x}＜\frac{3-x}{2}$；
（2）求证：$\sum_{k=1}^n{\frac{2}{2k+1}}≤\frac{2}{3}+ln\frac{n+1}{2}\;（n∈N，n≥2）$；
（3）若$?{x_1}，{x_2}∈[{e，{e^2}}]$，使f（x1）-f′（x2）≤a成立，求实数a的取值范围．
14．已知函数f（x）=lnx-$\frac{a}{x}$．
（1）当a＞0时，求f（x）在[e，+∞）上的最小值；
（2）若f（x）在[1，e]上的最小值为$\frac{3}{2}$，求实数a的值；
（3）若f（x）＜x2在（1，+∞）上恒成立，求a的取值范围．
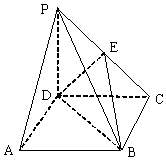15．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，E是PC的中点．
（1）证明：PA∥平面EDB；
（2）证明：BC⊥DE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网