题目内容
正方体ABCD-A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到对角线BC1的距离相等,则点P的轨迹是 .
考点:轨迹方程
专题:综合题
分析:作PM⊥AD、PE⊥BC、EF⊥BC1,连接PF,由线面垂直的判定定理、定义可得:PF是P到BC1的距离,以D为原点,AD所在直线为x轴,DC所在直线为y轴建立直角坐标系,利用条件建立方程,化简后判断出点P的轨迹.
解答:
解:假设正方体边长为1,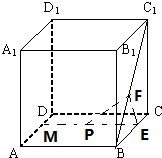
作PM⊥AD、PE⊥BC、EF⊥BC1,连接PF,
因为PE⊥CC1,BC∩CC1=C,所以PE⊥平面BCB1C1,
则PE⊥BC1,又EF⊥BC1,PE∩EF=E,
所以BC1⊥平面PEF,则BC1⊥PF,
所以PF是P到对角线BC1的距离,
以D为原点,AD所在直线为x轴,DC所在直线为y轴建立直角坐标系;
设任意一点P(x,y),到直线AD距离为|y|,到BC的距离PE=1-y,
在RT△BEF中,BE=1-x,EF=
(1-x),
在RT△PEF中,PF=
=
,
因为P到棱AD的距离与到对角线BC1的距离相等,
所以|y|=
,
化简得,(x-1)2=-4y+2(y≤
),
所以点P的轨迹是抛物线,
故答案为:抛物线.

作PM⊥AD、PE⊥BC、EF⊥BC1,连接PF,
因为PE⊥CC1,BC∩CC1=C,所以PE⊥平面BCB1C1,
则PE⊥BC1,又EF⊥BC1,PE∩EF=E,
所以BC1⊥平面PEF,则BC1⊥PF,
所以PF是P到对角线BC1的距离,
以D为原点,AD所在直线为x轴,DC所在直线为y轴建立直角坐标系;
设任意一点P(x,y),到直线AD距离为|y|,到BC的距离PE=1-y,
在RT△BEF中,BE=1-x,EF=
| ||
| 2 |
在RT△PEF中,PF=
| |PE|2+|EF|2 |
(1-y)2+[
|
因为P到棱AD的距离与到对角线BC1的距离相等,
所以|y|=
(1-y)2+[
|
化简得,(x-1)2=-4y+2(y≤
| 1 |
| 2 |
所以点P的轨迹是抛物线,
故答案为:抛物线.
点评:本题考查轨迹方程以及轨迹,线面垂直的判定定理、定义,考查学生分析解决问题的能力,确定轨迹方程是关键.

练习册系列答案
相关题目
若角A为三角形ABC的一个内角,且sinA+cosA=
,则这个三角形的形状为( )
| 11 |
| 25 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形 |
sinα=
,则sin2α-cos2α的值为( )
| ||
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知集合A={x|x2-3x+2=0},集合B={x|x>-1},则A∩B=( )
| A、(1,2) | B、{2} |
| C、{-1,2} | D、{1,2} |
cos
-tan
+
tan2
+sin
+cos2
+sin
的值等于( )
| π |
| 3 |
| 5π |
| 4 |
| 3 |
| 4 |
| π |
| 6 |
| 11π |
| 6 |
| 7π |
| 6 |
| 3π |
| 2 |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、-
|
已知约束条件
,且目标函数z=x-2y的最大值是4,则z的最小值是( )
|
| A、-2 | B、-7 | C、-3 | D、-5 |
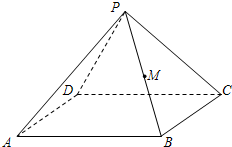 四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点
四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点