题目内容
若直线y=k(x+1)(k>0)与抛物线y2=4x相交于A,B两点,且A,B两点在抛物线的准线上的射影分别是M,N,若|BN|=2|AM|,则k的值是 .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:直线y=k(x+1)(k>0)恒过定点P(-1,0),由此推导出|OA|=
|BF|,由此能求出点A的坐标,从而能求出k的值.
| 1 |
| 2 |
解答:
解:设抛物线C:y2=4x的准线为l:x=-1
直线y=k(x+1)(k>0)恒过定点P(-1,0),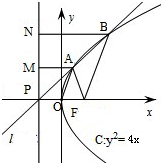
过A、B分别作AM⊥l于M,BN⊥l于N,
由|BN|=2|AM|,则|BF|=2|AF|,
∴点A为BP的中点.
连接OA,则|OA|=
|BF|,
∴|OA|=|AF|,
∴点A的横坐标为
,
∴点A的坐标为(
,
),
把(
,
)代入直线l:y=k(x+1)(k>0),
解得k=
.
故答案为:
.
直线y=k(x+1)(k>0)恒过定点P(-1,0),

过A、B分别作AM⊥l于M,BN⊥l于N,
由|BN|=2|AM|,则|BF|=2|AF|,
∴点A为BP的中点.
连接OA,则|OA|=
| 1 |
| 2 |
∴|OA|=|AF|,
∴点A的横坐标为
| 1 |
| 2 |
∴点A的坐标为(
| 1 |
| 2 |
| 2 |
把(
| 1 |
| 2 |
| 2 |
解得k=
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查直线与圆锥曲线中参数的求法,考查抛物线的性质,是中档题,解题时要注意等价转化思想的合理运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
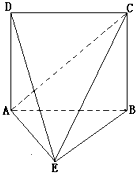 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=