题目内容
已知函数f(x)=x3+ax2+bx+1,曲线y=f(x)在(1,f(1))处的切线方程为y=4x-1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数y=f(x)的图象与直线y=kx-1有三个公共点,求k的取值范围.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数y=f(x)的图象与直线y=kx-1有三个公共点,求k的取值范围.
考点:函数解析式的求解及常用方法,利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:(Ⅰ)由题意可得f′(1)=3+2a+b=4,f(1)=2+a+b=3,联立方程组解得ab可得;
(Ⅱ)问题转化为g(x)=x2+
+1与y=k的交点问题,导数法判g(x)的单调性,数形结合可得.
(Ⅱ)问题转化为g(x)=x2+
| 2 |
| x |
解答:
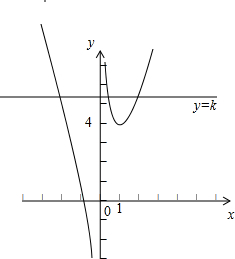 解:(Ⅰ)∵f(x)=x3+ax2+bx+1,∴f′(x)=3x2+2ax+b,
解:(Ⅰ)∵f(x)=x3+ax2+bx+1,∴f′(x)=3x2+2ax+b,
由题意可得f′(1)=3+2a+b=4,f(1)=2+a+b=3,
联立解得a=0,b=1,
∴函数f(x)的解析式为f(x)=x3+x+1;
(Ⅱ)由(Ⅰ)可得f(x)=x3+x+1,联立y=kx-1可得x3+(1-k)x+2=0,
易得x=0不是方程的解,故k=x2+
+1,
设g(x)=x2+
+1,则g′(x)=2x-
=
,
令g′(x)=0可得x=1,
可得当x∈(1,+∞)时,g′(x)>0,∴g(x)在(1,+∞)上单调递增;
当x∈(0,1)时,g′(x)<0,∴g(x)在(0,1)上单调递减;
当x∈(-∞,0)时,g′(x)<0,∴g(x)在(-∞,0)上单调递减;
∴g(x)的大致图象如图所示,g(1)=4是函数的极小值,
结合图象可知当k>4时,直线y=k和函数g(x)恰有三个公共点,
即函数y=f(x)的图象与直线y=kx-1有三个公共点.
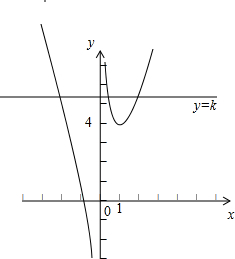 解:(Ⅰ)∵f(x)=x3+ax2+bx+1,∴f′(x)=3x2+2ax+b,
解:(Ⅰ)∵f(x)=x3+ax2+bx+1,∴f′(x)=3x2+2ax+b,由题意可得f′(1)=3+2a+b=4,f(1)=2+a+b=3,
联立解得a=0,b=1,
∴函数f(x)的解析式为f(x)=x3+x+1;
(Ⅱ)由(Ⅰ)可得f(x)=x3+x+1,联立y=kx-1可得x3+(1-k)x+2=0,
易得x=0不是方程的解,故k=x2+
| 2 |
| x |
设g(x)=x2+
| 2 |
| x |
| 2 |
| x2 |
| 2(x3-1) |
| x2 |
令g′(x)=0可得x=1,
可得当x∈(1,+∞)时,g′(x)>0,∴g(x)在(1,+∞)上单调递增;
当x∈(0,1)时,g′(x)<0,∴g(x)在(0,1)上单调递减;
当x∈(-∞,0)时,g′(x)<0,∴g(x)在(-∞,0)上单调递减;
∴g(x)的大致图象如图所示,g(1)=4是函数的极小值,
结合图象可知当k>4时,直线y=k和函数g(x)恰有三个公共点,
即函数y=f(x)的图象与直线y=kx-1有三个公共点.
点评:本题考查函数解析式的求解和导数法判函数的单调性,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,若
=a1
+a200
,且A、B、C三点共线(该直线不过点O),则S200等于( )
| OB |
| OA |
| OC |
| A、100 | B、200 |
| C、101 | D、201 |
若等差数列{an}有两项am和ak(m≠k),满足am=
,ak=
,则该数列前mk项之和为( )
| 1 |
| k |
| 1 |
| m |
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线l与直线y=1,x=7分别交于点P、Q,且线段PQ的中点坐标为(1,-1),则直线l的斜率为( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
函数f(x)=sinx在区间[a,b]上是增函数,且f(a)=-1,f(b)=1,则cos
的值为( )
| a+b |
| 2 |
| A、-1 | ||||
| B、0 | ||||
C、
| ||||
| D、1 |