题目内容
若函数y=f（x）满足f（x-1）=1-2x+x2，则y′=f′（x）= ．
考点：导数的运算
专题：导数的概念及应用
分析：求出函数的表达式，利用函数的导数公式进行求解即可．
解答：
解：设t=x-1，则f（x-1）=1-2x+x2=（x-1）2，
即f（t）=t2，
则f（x）=x2，
则f′（x）=2x，
故答案为：2x
即f（t）=t2，
则f（x）=x2，
则f′（x）=2x，
故答案为：2x
点评：本题主要考查导数的计算，利用换元法求出函数的解析式是解决本题的关键．
练习册系列答案
春雨教育同步作文系列答案
相关题目
与函数y=x为相同函数的是（ ）
A、y=
| ||
B、y=
| ||
| C、y=elnx | ||
| D、y=log22x |
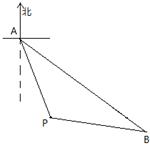如图，某船在A处看见灯塔P在南偏东15°方向，后来船沿南偏东45°的方向航行30km后，到达B处，看见灯塔P在船的西偏北15°方向，则这时船与灯塔的距离是（ ）| A、10km | ||
| B、20km | ||
C、10
| ||
D、5
|
已知直线l1：y=x+1，l2：y=mx+2当l1⊥l2时，则m等于（ ）
| A、0 | B、-3 | C、-1 | D、1 |
抛掷一个骰子，记A为事件“落地时向上的数为奇数”，B为事件“落地时向上的数是偶数”，C为事件“落地时向上的数是3的倍数”，下面是对立事件的是（ ）
| A、A与B | B、A与C |
| C、B与C | D、A、B与C |