题目内容
设
,
为两个不共线向量,若
=x
+y
,其中x,y为实数,则记
=[x,y].已知两个非零向量
,
满足
=[x1,y1],
=[x2,y2],则下述四个论断中正确的序号为 .(所有正确序号都填上)
①
+
=[x1+x2,y1+y2];
②λ
=[λx1,λy1],其中λ∈R;
③
∥
?x1y2=x2y1;
④
⊥
?x1x2+y1y2=0.
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| a |
| m |
| n |
| m |
| n |
①
| m |
| n |
②λ
| m |
③
| m |
| n |
④
| m |
| n |
考点:命题的真假判断与应用,平行向量与共线向量,平面向量数量积的运算
专题:平面向量及应用
分析:直接利用向量的运算法则求解,推出结果判断谢谢即可.
解答:
解:设
,
为两个不共线向量,若
=x
+y
,其中x,y为实数,则记
=[x,y].
已知两个非零向量
,
满足
=[x1,y1],
=[x2,y2],
①
+
=x1
+y1
+x2
+y2
=(x1+x2)
+(y1+y2)
,
所以
+
=[x1+x2,y1+y2];①正确;
λ
=λ(x1
+y1
)=λx1
+λy1
,所以λ
=[λx1,λy1],其中λ∈R;②正确;
③
∥
?
=
?x1y2=x2y1;③正确;
④
•
=(x1
+y1
)(x2
+y2
)=x1x2+y1y2+(x1y2+x2y1)
•
=0.
所以④不正确.
故答案为:①②③.
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| a |
已知两个非零向量
| m |
| n |
| m |
| n |
①
| m |
| n |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
所以
| m |
| n |
λ
| m |
| e1 |
| e2 |
| e1 |
| e2 |
| m |
③
| m |
| n |
| x1 |
| y1 |
| x2 |
| y2 |
④
| m |
| n |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
所以④不正确.
故答案为:①②③.
点评:本题考查向量的基本运算,向量平行与垂直体积的应用,基本知识的考查.

练习册系列答案
相关题目
 在如图所示的程序框图中,输入A=192,B=22,则输出的结果是( )
在如图所示的程序框图中,输入A=192,B=22,则输出的结果是( )| A、0 | B、2 | C、4 | D、6 |
各项均为正数的数列{an},{bn}满足:an+2=2an+1+an,bn+2=bn+1+2bn(n∈N*),那么( )
| A、?n∈N*,an>bn⇒an+1>bn+1 |
| B、?m∈N*,?n>m,an=bn |
| C、?m∈N*,?n>m,an>bn |
| D、?m∈N*,?n>m,an<bn |
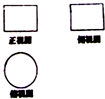 如图所示的是一个立体图形的三视图,此立体图形的名称为:
如图所示的是一个立体图形的三视图,此立体图形的名称为: