题目内容
已知不等式组
表示的平面区域的面积为9,点P(x,y)在所给平面区域内,则z=3x+y的最大值为 .
|
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,先求出a,再将z=3x+y化为y=-3x+z,z相当于直线y=-3x+z的纵截距,由几何意义可得.
解答:
解:由题意作出其平面区域,

故由题意知,
×a×2a=9;
故a=3;
则z=3x+y化为y=-3x+z,z相当于直线y=-3x+z的纵截距,
由图可得,
当过点(3,3)时有最大值,
即z=3×3+3=12.
故答案为:12.

故由题意知,
| 1 |
| 2 |
故a=3;
则z=3x+y化为y=-3x+z,z相当于直线y=-3x+z的纵截距,
由图可得,
当过点(3,3)时有最大值,
即z=3×3+3=12.
故答案为:12.
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
相关题目
阅读如图的程序框图,若输入的n是100,则输出的变量S的值是( )


| A、5 049 |
| B、5 050 |
| C、5 051 |
| D、5 052 |
椭圆C:
+
=1(a>b>0)的右焦点为F,椭圆C与x轴正半轴交于A点,与y轴正半轴交于B(0,2),且
•
=4
+4,则椭圆C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| BF |
| BA |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
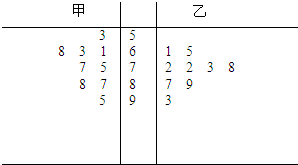 某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图
某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图