题目内容
1.已知抛物线y2=4x的焦点为F,其准线与x轴交于点H,点P在抛物线上,且$|PH|=\sqrt{2}|PF|$,则点P的横坐标为1.分析 过P作PE垂直于准线与E,由抛物线的定义得|PE|=|PF|;通过$|PH|=\sqrt{2}|PF|$,即可得到结论.
解答  解:过P作PE垂直于准线与E.
解:过P作PE垂直于准线与E.
由抛物线的定义得:|PE|=|PF|.
抛物线y2=4x的焦点为F,其准线与x轴交于点H,点P在抛物线上,在Rt△EPH中,$|PH|=\sqrt{2}|PF|$,
所以EPFH是正方形.抛物线y2=4x的焦点为F(1,0),
则点P的横坐标为:1.
故答案为:1.
点评 本题主要考查抛物线的简单性质.解题的关键在于利用抛物线的定义得到|NE|=|NF|.

练习册系列答案
相关题目
9.已知集合A={x∈R||x|≥2},B={x∈R|x2-x-2<0},则下列结论正确的是( )
| A. | A∪B=R | B. | A∩B≠∅ | C. | A∪B=∅ | D. | A∩B=∅ |
11.双曲线x2-4y2=4的渐近线方程是( )
| A. | y=±4x | B. | y=±$\frac{1}{4}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
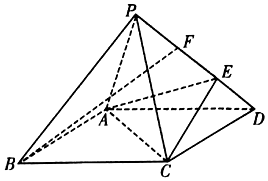 18、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.
18、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.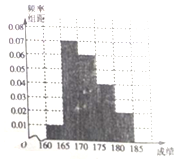 某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:
某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示: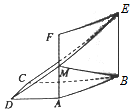 如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,
如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,