题目内容
选修4—5:不等式选讲
设函数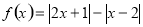
(1)求不等式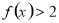 的解集;
的解集;
(2)若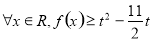 恒成立,求实数
恒成立,求实数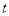 的取值范围.
的取值范围.
(1) ;(2)
;(2)
【解析】
试题分析:(1)由题意得 ,
,
当 时,不等式化为-x-3>2,解得x<-5,∴x<-5,
时,不等式化为-x-3>2,解得x<-5,∴x<-5,
当 时,不等式化为3x-1>2,解得x>1,∴1<x<2,
时,不等式化为3x-1>2,解得x>1,∴1<x<2,
当x≥2时,不等式化为x+3>2,解得x>-1,∴x≥2,
综上,不等式的解集为 .
.
(2)由(1)得 ,若
,若 x∈R,
x∈R, 恒成立,
恒成立,
则只需 ,解得
,解得 ,
,
综上,t的取值范围为
考点:本题考查绝对值不等式,恒成立的问题

练习册系列答案
相关题目

 B.
B. C.
C. D.
D.
 满足条件
满足条件 ,则
,则 的取值范围为
的取值范围为 B.
B. C.
C. D.
D.
 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图像关于点
的图像关于点 对称,
对称, 、
、 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的
的 B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.
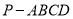 中,
中,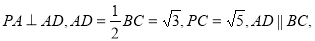
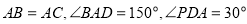
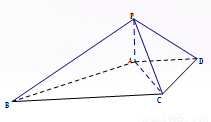
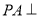 平面
平面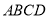
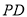 上是否存在一点
上是否存在一点 ,使直线
,使直线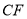 与平面
与平面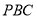 成角正弦值等于
成角正弦值等于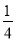 ,若存在,指出点
,若存在,指出点 中,
中, ,映射
,映射 将
将 对应到
对应到 上的点
上的点 ,则当点
,则当点 沿着折线
沿着折线 运动时,在映射
运动时,在映射 的轨迹是( )
的轨迹是( )


 名学生被考官L面试,求
名学生被考官L面试,求 的分布列和数学期望.
的分布列和数学期望. 表示的平面区域,并求平面区域面积。
表示的平面区域,并求平面区域面积。