题目内容
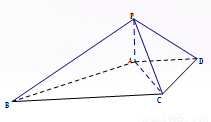
如图:四棱锥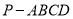 中,
中,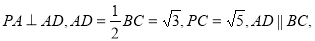
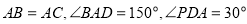
(1)证明: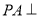 平面
平面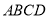
(2)在线段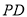 上是否存在一点
上是否存在一点 ,使直线
,使直线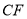 与平面
与平面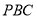 成角正弦值等于
成角正弦值等于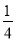 ,若存在,指出点
,若存在,指出点 位置,
位置,
若不存在,请说明理由.
(1)见解析:(2)点F是线段PD的中点
【解析】
试题分析:
(Ⅰ)证明:取线段BC中点E,连结AE.
因为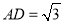 ,
,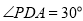 ,所以PA=1 1分
,所以PA=1 1分
因为AD∥BC,∠BAD=150°,所以∠B=30°, 2分
又因为AB=AC,所以AE⊥BC,而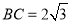
所以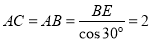 . 4分
. 4分
因为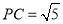 ,所以
,所以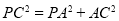 即PA⊥AC
即PA⊥AC
因为PA⊥AD,且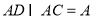
所以PA⊥平面ABCD 6分
(Ⅱ)
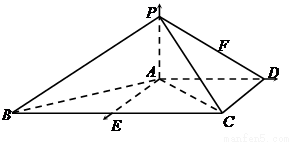
【解析】
以A为坐标原点,以AE,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系如图所示:
则: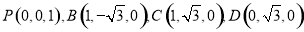 8分
8分
设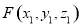 ;平面PBC的法向量
;平面PBC的法向量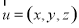 .
.
因为点F在线段PD上,所以假设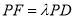 ,所以
,所以
即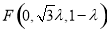 ,所以
,所以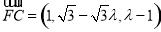 . 9分
. 9分
又因为平面PBC的法向量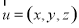 .
.
所以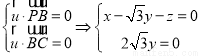
所以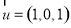 10分
10分
因为直线CF与平面PBC成角正弦值等于 ,所以
,所以 .
.
解得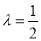 .所以点F是线段PD的中点.
.所以点F是线段PD的中点.
考点:本题考查线面垂直的判定,线面角

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 时,求
时,求 的极值;
的极值;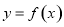 上的两个不同点,且曲线在A、B两点处的切线均与
上的两个不同点,且曲线在A、B两点处的切线均与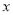 轴平行,直线AB的斜率为
轴平行,直线AB的斜率为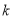 ,是否存在
,是否存在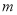 ,使得
,使得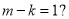 若存在,请求出
若存在,请求出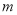 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. 等于
等于 B.
B.
 D.
D.
 中,
中, ,且
,且 ,则
,则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
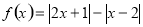
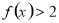 的解集;
的解集;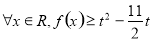 恒成立,求实数
恒成立,求实数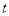 的取值范围.
的取值范围. 在点
在点 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,则
,则 的值为
的值为 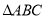 的边长为
的边长为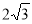 ,平面内一点
,平面内一点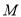 满足:
满足: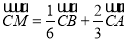 ,
,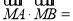 ( )
( )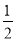 a3,2a2成等差数列,则
a3,2a2成等差数列,则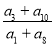 =________.
=________.