题目内容
10．
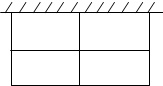如图，动物园要围成相同面积的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．现有可围36m长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼的面积最大？
分析 设出每间虎笼的长和宽，利用周长为定值，根据基本不等式，求出面积最大时的长与宽的值．
解答 解：设每间虎笼的长、宽各设计为xm，ym时，可使每间虎笼的面积最大，
则4x+6y=36，S=xy；
∵4x+6y=36，∴2x+3y=18，
由基本不等式，得18≥2$\sqrt{2x•3y}$，
∴xy≤$\frac{27}{2}$，
当且仅当2x=3y=9，即x=4.5m，y=3m时，S取得最大值$\frac{27}{2}$；
即每间虎笼的长、宽各设计为4.5m，3m时，可使每间虎笼的面积最大；
且最大值为$\frac{27}{2}$．
点评 本题考查了利用数学模型解决实际应用问题，也考查了基本不等式的运用问题，是中档题．
练习册系列答案
相关题目
18．抛物线y2=2px（p＞0）的焦点为F，点A，B在抛物线上，且满足∠AFB=$\frac{2π}{3}$，过弦AB的中点P作抛物线准线的垂线PM，垂足为M，则$\frac{|PM|}{|AB|}$的最大值为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | 1 | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |
19．下列各组函数中，f（x）与g（x）表示同一个函数的是（ ）
| A． | $f（x）=x，g（x）=\sqrt{x^2}$ | B． | $f（x）=x，g（x）=\root{3}{x^3}$ | ||
| C． | f（x）=x，g（x）=（x-1）0 | D． | $f（x）=\frac{{{x^2}-9}}{x+3}，g（x）=x-3$ |