题目内容
2.(Ⅰ)计算:1.5${\;}^{-\frac{1}{3}}$×(-$\frac{7}{6}$)0+80.25×$\root{4}{2}$+($\root{3}{2}$×$\sqrt{3}$)6-$\sqrt{(\frac{2}{3})^{\frac{2}{3}}}$的值.(Ⅱ)计算:lg22•lg250+lg25•lg40的值.
分析 (Ⅰ)利用有理数指数幂性质、运算法则求解.
(Ⅱ)利用对数性质、运算法则求解.
解答 解:(Ⅰ)1.5${\;}^{-\frac{1}{3}}$×(-$\frac{7}{6}$)0+80.25×$\root{4}{2}$+($\root{3}{2}$×$\sqrt{3}$)6-$\sqrt{(\frac{2}{3})^{\frac{2}{3}}}$
=$\frac{{2}^{\frac{1}{3}}}{{3}^{\frac{1}{3}}}$×1+${2}^{\frac{3}{4}}$×2${\;}^{\frac{1}{4}}$+4×27-($\frac{2}{3}$)${\;}^{\frac{1}{3}}$
=2+108
=110.
(Ⅱ)lg22•lg250+lg25•lg40
=lg22(2lg5+1)+lg25(2lg2+1)
=2lg22lg5+lg22+2lg25lg2+lg25
=2lg2lg5(lg2+lg5)+lg22+lg25
=lg22+2lg2lg5+lg25
=(lg2+lg5)2
=1.
点评 本题考查对数式、指数式化简求值,是基础题,解题时要认真审题,注意指数、对数的性质和运算法则的合理运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.已知p,q满足p+2q-1=0,则直线px+3y+q=0必过定点( )
| A. | $(-\frac{1}{6},\frac{1}{2})$ | B. | $(\frac{1}{2},\frac{1}{6})$ | C. | $(\frac{1}{2},-\frac{1}{6})$ | D. | $(\frac{1}{6},-\frac{1}{2})$ |
13.下列对应是从集合S到T的映射的是( )
| A. | S=N,T={-1,1},对应法则是n→(-1)n,n∈S | |
| B. | S={x|x∈R},T={y|y∈R},对应法则是x→y=$\frac{1+x}{1-x}$ | |
| C. | S={0,1,2,5},T={1,$\frac{1}{2}$,$\frac{1}{5}$},对应法则是取倒数 | |
| D. | S={0,1,4,9},T={-3,-2,-1,0,1,2,3},对应法则是开平方. |
7.在△ABC中,a=2,b=3,A=$\frac{π}{6}$,则cosB的值为( )
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{\sqrt{7}}{4}$ | D. | ±$\frac{4}{5}$ |
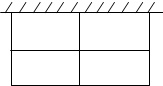 如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?