题目内容
20.若x>1,则函数y=$\frac{{x}^{2}-x+1}{x-1}$的最小值为3.分析 换元可得t=x-1>0,可得x=t+1,代入可得y=t+$\frac{1}{t}$+1,由基本不等式可得.
解答 解:∵x>1,∴t=x-1>0,解得x=t+1,
∴y=$\frac{{x}^{2}-x+1}{x-1}$=$\frac{(t+1)^{2}-(t+1)+1}{t}$
=$\frac{{t}^{2}+t+1}{t}$=t+$\frac{1}{t}$+1≥2$\sqrt{t•\frac{1}{t}}$+1=3,
当且仅当t=$\frac{1}{t}$即t=1即x=2时取等号.
故答案为:3.
点评 本题考查基本不等式求最值,整体换元是解决问题的关键,属基础题.

练习册系列答案
相关题目
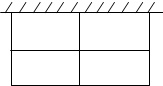 如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大? 在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )
在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )