题目内容
20．直线l的方程为3x-2y+6=0，则直线l在x轴上的截距是-2；y轴上的截距是3．分析 直线l：3x-2y+6=0中，令y=0，求出x的值直线l在x轴上的截距；令x=0，求出的y的值是直线l在y轴上的截距．
解答 解：∵直线l的方程为3x-2y+6=0，
∴当y=0时，解得x=-2，
当x=0时，解得y=3，
∴直线l在x轴上的截距是-2，y轴上的截距是3．
故答案为：-2，3．
点评 本题考查直线方程的横截距和纵截距的求法，是基础题，令y=0，求出x的值直线l在x轴上的截距；令x=0，求出的y的值是直线l在y轴上的截距．
练习册系列答案
相关题目
5．若全集U={0，1，2，3，4}且∁UA={2，4}，则集合A的真子集共有（ ）个．
| A． | 8个 | B． | 7个 | C． | 4个 | D． | 3个 |
12．已知p，q满足p+2q-1=0，则直线px+3y+q=0必过定点（ ）
| A． | $（-\frac{1}{6}，\frac{1}{2}）$ | B． | $（\frac{1}{2}，\frac{1}{6}）$ | C． | $（\frac{1}{2}，-\frac{1}{6}）$ | D． | $（\frac{1}{6}，-\frac{1}{2}）$ |
9．将函数f（x）=cos2x的图象向左平移$\frac{π}{3}$个单位得到函数g（x）的图象，则函数g（x）（ ）
| A． | 一个对称中心是（-$\frac{π}{3}$，0） | B． | 一条对称轴方程为x=$\frac{π}{3}$ | ||
| C． | 在区间[-$\frac{π}{3}$，0]上单调递减 | D． | 在区间[0，$\frac{π}{3}$]上单调递增 |
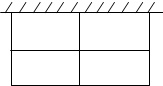如图，动物园要围成相同面积的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．现有可围36m长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼的面积最大？