题目内容
10．已知集合A={x|2x2-7x+3＜0}，B={x∈Z|lgx＜1}，则阴影部分表示的集合的元素个数为（ ）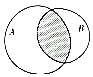
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据图所示的阴影部分所表示的集合的元素属于集合A但不属于集合B，即求A∩B，根据交集的定义和补集的定义即可求得
解答 解：阴影部分所表示的集合为A∩B，
A={x|2x2-7x+3＜0}=（$\frac{1}{2}$，3），
B={x∈Z|lgx＜1}={x∈Z|0＜x＜10}，
A∩B={1，2}，
那么满足图中阴影部分的集合的元素的个数为2，
故选B
点评 本题主要考查了Venn图表达集合的关系及运算，同时考查了识图能力和分析问题的能力，属于基础题．
练习册系列答案
相关题目
20．在区间[-3，3]上随机选取一个实数x，则事件“2x-3＜0”发生的概率是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
1．已知双曲线Γ：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一条渐近线为l，圆C：（x-a）2+y2=8与l交于A，B两点，若△ABC是等腰直角三角形，且$\overrightarrow{OB}=5\overrightarrow{OA}$（其中O为坐标原点），则双曲线Γ的离心率为（ ）
| A． | $\frac{{2\sqrt{13}}}{3}$ | B． | $\frac{{2\sqrt{13}}}{5}$ | C． | $\frac{{\sqrt{13}}}{5}$ | D． | $\frac{{\sqrt{13}}}{3}$ |
18．某几何体的三视图如图，则该几何体的体积为（ ）
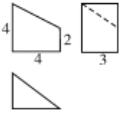
| A． | 18 | B． | 20 | C． | 24 | D． | 12 |
15．双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的两条渐近线互相垂直，F1，F2分别为C的左，右焦点，P点在该双曲线的右支上且到直线x=-$\frac{{\sqrt{2}}}{2}$a的距离为3$\sqrt{2}$，若|PF1|+|PF2|=8，则双曲线的标准方程为（ ）
| A． | $\frac{x^2}{4}-\frac{y^2}{4}=1$ | B． | $\frac{x^2}{8}-\frac{y^2}{8}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{16}=1$ | D． | 以上答案都不对 |
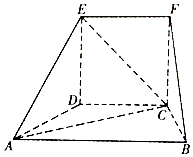在如图所示的几何体中，四边形CDEF为正方形，四边形ABCD为等腰梯形，AB∥CD，AB=2BC，∠BAC=30°，AC⊥FB．