题目内容
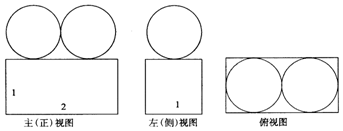
13．某三棱柱的三视图如图所示，该三棱柱的表面积为3+2$\sqrt{5}$．
分析 由已知得到几何体为平放的三棱柱，根据图中数据计算表面积．
解答 
解：由已知得到几何体如图：三棱柱的表面积为$\frac{1}{2}×2×1×2+1×1+2×1+\sqrt{5}×1$=3+2$\sqrt{5}$；
故答案为：3+2$\sqrt{5}$．
点评 本题考查了由几何体的三视图求几何体的表面积；关键是正确还原几何体．
练习册系列答案
相关题目
3．不等式组$\left\{{\begin{array}{l}{y≤x}\\{3y≥x}\\{x+y≥4}\end{array}}\right.$的解集记为D，命题p：?（x，y）∈D，x+2y≥5，命题q：?（x，y）∈D，2x-y＜2，则下列命题为真命题的是（ ）
| A． | ?p | B． | q | C． | p∨（?q） | D． | （?p）∨q |
4．一个空间几何体的三视图如下，则这个空间几何体的体积是（ ）
| A． | 2+$\frac{4π}{3}$ | B． | 2+$\frac{π}{3}$ | C． | 1+$\frac{4π}{3}$ | D． | 10+8π |
8．濮阳市黄河滩区某村2010年至2016年人均纯收入（单位：万元）的数据如下表：
（Ⅰ）求y关于x的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2010年至2016年该村人均纯收入的变化情况，并预测该村2017年人均纯收入．
附：回归直线的斜率和截距的最小乘法估计公式分别为：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$．
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（Ⅱ）利用（Ⅰ）中的回归方程，分析2010年至2016年该村人均纯收入的变化情况，并预测该村2017年人均纯收入．
附：回归直线的斜率和截距的最小乘法估计公式分别为：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$．
18．用反证法证明“a、b∈N*，如果a、b能被2017整除，那么a、b中至少有一个能被2017整除”时，假设的内容是（ ）
| A． | a不能被2017整除 | B． | b不能被2017整除 | ||
| C． | a、b都不能被2017整除 | D． | a、b中至多有一个能被2017整除 |
6．设A（x1，y1），B（x2，y2），C（x3，y3）为平面上不共线的三点，则三角形ABC的面积为（ ）
| A． | $\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$| | B． | $\frac{1}{2}$$|\begin{array}{l}{{x}_{1}}&{{y}_{1}}&{1}\\{{x}_{2}}&{{y}_{2}}&{1}\\{{x}_{3}}&{{y}_{3}}&{1}\end{array}|$ | ||
| C． | $\frac{1}{2}$|$\overrightarrow{AB}$$•\overrightarrow{AC}$| | D． | $\frac{1}{2}$（cos|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|） |