题目内容
1.以下是某样本数据,则该样本的中位数、极差分别是( )| 数据 | 31,12,22,15,20,45,47,32,34,23,28 |
| A. | 23、32 | B. | 34、35 | C. | 28、32 | D. | 28、35 |
分析 将数据从小到大按顺序排成一列,结合中位线和极差的定义进行求解即可.
解答 解:将数据从小到大按顺序排成一列为12,15,20,22,23,28,31,32,34,45,47,共11个数据,
则中位数为第6个数28,最大值为47,最小值为12,则极差47-12=35,
故选:D.
点评 本题主要考查中位线和极差的计算,根据条件将数据从小到大进行排列是解决本题的关键.

练习册系列答案
相关题目
12.已知函数f(x)=(2x-1)ex,a=f(1),b=f(-$\sqrt{2}$),c=f(-ln2),d=f(-$\frac{1}{2}$),则( )
| A. | a>b>c>d | B. | b>a>c>d | C. | d>a>b>c | D. | a>d>c>b |
9.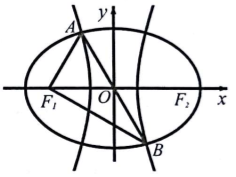 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
15.函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2-x)>0的解集为( )
| A. | {x|-2<x<2} | B. | {x|x>2,或x<-2} | C. | {x|0<x<4} | D. | {x|x>4,或x<0} |

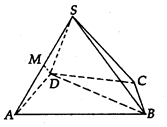 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.