题目内容
函数f（x）=ex+3x的零点个数是 ．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：根据零点的判断定理，即可求出函数f（x）的零点个数．
解答：
解：∵f（x）=ex+3x为增函数，
∵f（0）=1＞0，f（-1）=e-1-3＜0，
∴在（-1，0）内函数f（x）存在唯一的一个零点，
即零点的个数为1个，
故答案为：1
∵f（0）=1＞0，f（-1）=e-1-3＜0，
∴在（-1，0）内函数f（x）存在唯一的一个零点，
即零点的个数为1个，
故答案为：1
点评：本题主要考查函数零点个数的判断，函数零点的判断条件是解决本题的关键．
练习册系列答案
相关题目
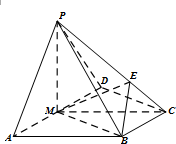如图，在四棱锥P-ABCD中，侧面PAD是正三角形，底面ABCD是直角梯形，AD∥BC，∠ADC=90°，AD=2BC=2，CD=
如图，扇形AOB的弧的中点为M，动点C，D分别在线段OA，OB上，且BD=2OC．若OA=2，∠AOB=120°，则