题目内容
19.若(x+1)n=xn+…+ax3+bx2+…+1(n∈N*),且a:b=3:1,则n的值为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 x+1)n=xn+…+ax3+bx2+…+1(n∈N*),可得:a=${∁}_{n}^{n-3}$,b=${∁}_{n}^{n-2}$,利用a:b=3:1,及其组合数的计算公式即可得出.
解答 解:(x+1)n=xn+…+ax3+bx2+…+1(n∈N*),
可得:a=${∁}_{n}^{n-3}$,b=${∁}_{n}^{n-2}$,又a:b=3:1,
化为:${∁}_{n}^{3}$:${∁}_{n}^{2}$=3:1,化为n-2=9,解得n=11.
故选:C.
点评 本题考查了二项式定理的通项公式及其组合数的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
10.欲证$\sqrt{7}$-1>$\sqrt{11}$-$\sqrt{5}$,只需证( )
| A. | ${(\sqrt{7}-1)^2}>{(\sqrt{11}-\sqrt{5})^2}$ | B. | ${(\sqrt{7}+1)^2}>{(\sqrt{11}+\sqrt{5})^2}$ | C. | ${(\sqrt{7}+\sqrt{5})^2}>{(\sqrt{11}+1)^2}$ | D. | ${(\sqrt{7}-\sqrt{5})^2}>{(\sqrt{11}-1)^2}$ |
4.已知△ABC是一个圆锥的底面圆的内接三角形,AB=3,∠ACB=60°,母线与底面所成角的余弦值为$\frac{3}{5}$,则该圆锥的体积为( )
| A. | 8π | B. | 5π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 4$\sqrt{3}$π |
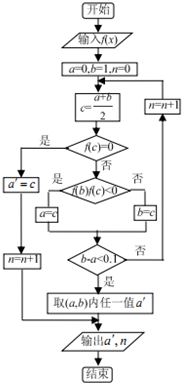 如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )
如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )