题目内容
已知一物体做 圆周运动,出发后 t分钟内走过的路程s=at2+bt(a≠0),最初用5分钟走完第一圈,接下去用3分钟走完第二圈.
(1)试问该物体走完第三圈用了多长时间?(结果可用无理数表示)
(2)(理科做文科不做)试问从第几圈开始,走完一圈的时间不超过1分钟?
(1)试问该物体走完第三圈用了多长时间?(结果可用无理数表示)
(2)(理科做文科不做)试问从第几圈开始,走完一圈的时间不超过1分钟?
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:(1)根据最初用5分钟走完第一圈,接下去用3分钟走完第二圈,确定圆周长、b、a的关系,再利用所给方程,即可求得走完第三圈的时间;
(2)设出发t分钟后走完第x圈,求出所需时间,从而可得走完第(x-1)圈需要时间,利用走完一圈的时间不超过1分钟,即可建立不等式,从而可得结论.
(2)设出发t分钟后走完第x圈,求出所需时间,从而可得走完第(x-1)圈需要时间,利用走完一圈的时间不超过1分钟,即可建立不等式,从而可得结论.
解答:
解:(1)设圆周长为l,则∵最初用5分钟走完第一圈,接下去用3分钟走完第二圈
∴
,∴
设出发t分钟后走完第三圈,则at2+bt=3l,∴上式代入可得t2+7t-180=0
∵t>0,∴t=
∴走完第三圈需要时间为t=
-8=
分钟;
(2)设出发t分钟后走完第x圈,则at2+7at=x•60a,∴t=
则走完第(x-1)圈,需要时间t′=
由题意,t-t′≤1,则
-
≤1
∴当x≥16时,不等式成立
∴从第16圈开始,走一圈所用时间不超过1分钟.
∴
|
|
设出发t分钟后走完第三圈,则at2+bt=3l,∴上式代入可得t2+7t-180=0
∵t>0,∴t=
| ||
| 2 |
∴走完第三圈需要时间为t=
| ||
| 2 |
| ||
| 2 |
(2)设出发t分钟后走完第x圈,则at2+7at=x•60a,∴t=
| ||
| 2 |
则走完第(x-1)圈,需要时间t′=
| ||
| 2 |
由题意,t-t′≤1,则
| ||
| 2 |
| ||
| 2 |
∴当x≥16时,不等式成立
∴从第16圈开始,走一圈所用时间不超过1分钟.
点评:本题考查利用函数关系式解决实际问题,考查学生的计算能力,考查解不等式,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设集合A,B是全集U的两个子集,则A
B是CUB
CUA的( )
| ? |
| ≠ |
| ? |
| ≠ |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
一颗正方体骰子,共六个面的点数分别是1、2、3、4、5、6,将这颗骰子连续掷三次观察向上的点数,则三次点数和为16的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
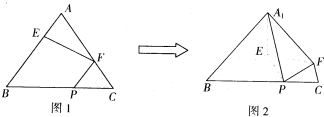 如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设
如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设