题目内容
已知双曲线
-
=1的左右焦点分别为F1，F2，过左焦点F1作直线l与双曲线左右两支分别交于A、B两点，若△ABF2为正三角形，则双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、±
| ||
B、x±
| ||
C、
| ||
D、x±
|
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的性质，结合△ABF2为正三角形，求出a，b，c的关系即可得到结论．
解答：
解：设|AB|=|BF2|=|AF2|=x，则由|BF1|-|BF2|=2a得|AF1|=2a，
又由|AF2|-|AF1|=2a，得|AF2|=x=4a，
∴△BF1F2中，|BF1|=6a，|BF2|=4a，|F1F2|=2c，结合余弦定理得，（2c）2=（6a）2+（4a）2-2×6a×4a×cos60°⇒4c2=28a2，得a2+b2=7a2，
=6，
渐近线方程为y=±
x．
故选A．
又由|AF2|-|AF1|=2a，得|AF2|=x=4a，
∴△BF1F2中，|BF1|=6a，|BF2|=4a，|F1F2|=2c，结合余弦定理得，（2c）2=（6a）2+（4a）2-2×6a×4a×cos60°⇒4c2=28a2，得a2+b2=7a2，
| b2 |
| a2 |
渐近线方程为y=±
| 6 |
故选A．
点评：本题主要考查双曲线的渐近线方程，根据双曲线的图象和性质是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
椭圆C：
+
=1（a＞b＞0）和双曲线D：
-
=1（A＞0，B＞0）有相同的焦点F1、F2，椭圆C和双曲线D在第一象限内的交点为P，且PF2垂直于x轴．设椭圆的离心率为e1，双曲线D的离心率为e2，则e1e2等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| A2 |
| y2 |
| B2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、不确定 |
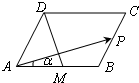在平行四边形ABCD中，AB=2，AD=1，∠DAB=60°，点M为AB的中点，点P从B→C→D（含端点），设∠PAB=α，记tanα=x，| AP |
| DM |
A、 |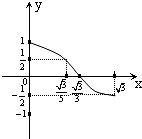
B、 |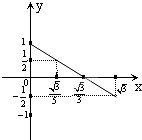
C、 |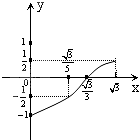
D、 |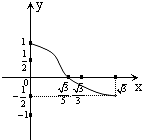
在△ABC中，A=60°，b=1，且面积为
，则
=（ ）
| 3 |
| 2a+2b-2c |
| sinA+sinB-sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
已知双曲线
-
=1的左、右焦点为F1，F2，过F1的直线垂直于x轴且与该双曲线相交于A，B两点，△ABF2 的内切圆经过点（0，a），则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
在回归模型中，预报变量的值与下列哪些因素有关（ ）
| A、受解释变量的影响与随机误差无关 |
| B、受随机误差的影响与解释变量无关 |
| C、与总偏差平方和有关与残差无关 |
| D、与解释变量和随机误差的总效应有关 |
若θ为锐角且cosθ-cos-1θ=-2，则cosθ+cos-1θ的值为（ ）
A、2
| ||
B、
| ||
| C、6 | ||
| D、4 |