题目内容
18.已知$\overrightarrow a=(1,0){,_{\;}}\overrightarrow b=(2,1)$,则$\overrightarrow a$•$\overrightarrow b$=2.分析 利用平面向量的数量积公式的坐标运算进行计算即可.
解答 解:由已知$\overrightarrow a=(1,0){,_{\;}}\overrightarrow b=(2,1)$,则$\overrightarrow a$•$\overrightarrow b$=1×2+0×1=2;
故答案为:2.
点评 本题考查了平面向量的数量积公式的坐标运算;熟记公式是关键.

练习册系列答案
相关题目
9.画边长为2的正方体ABCD-A1B1C1D1的三视图中的正视图时,若以△A1C1D所在的平面为投影面,则得到的正视图面积为( )
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
10.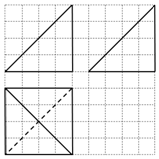 某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )
某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )
 某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )
某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )| A. | 16 | B. | 32 | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
8.已知函数f(x)=sin(x+$\frac{π}{2}$),g(x)=cos(x+π),则下列结论中正确的是( )
| A. | 将f(x)的图象向左平移$\frac{π}{2}$个单位后得到g(x)的图象 | |
| B. | 函数y=f(x)•g(x)的最小正周期为2π | |
| C. | 函数y=f(x)•g(x)的最大值为1 | |
| D. | x=$\frac{π}{2}$是函数y=f(x)•g(x)图象的一条对称轴 |