题目内容
在空间直角坐标系中，某几何体各定点的坐标分别为（0，0，0）、（2，0，0）、（2，2，0）、（0，2，0）、（0，0，1）、（2，2，1）、（0，2，2），则该几何体在xOz和yOz上的投影的面积分别为m、n，则m+n的值为（ ）
| A、7 | B、6 | C、5 | D、4 |
考点：空间中的点的坐标
专题：空间位置关系与距离
分析：该几何体如图所示，该几何体在xOz和yOz上的投影的面积分别为：直角梯形CDGF的面积，直角梯形ADGE的面积，计算即可得出．
解答：
解：该几何体如图所示，
该几何体在xOz和yOz上的投影的面积分别为：直角梯形CDGF的面积，直角梯形ADGE的面积，
∴m=n=
×(1+2)×2×2=6，
则m+n=6．
故选：B．
该几何体在xOz和yOz上的投影的面积分别为：直角梯形CDGF的面积，直角梯形ADGE的面积，
∴m=n=
| 1 |
| 2 |
则m+n=6．
故选：B．
点评：本题考查了几何体的三视图及其面积计算、空间中的点的坐标，属于基础题，
练习册系列答案
相关题目
图中阴影部分所表示的集合是（ ）
| A、B∩[∁U（A∪C）] |
| B、（B∪C）∩（∁UA） |
| C、（A∪C）∩（∁UB） |
| D、（∁UA）∩B |
若集合M={x|2-x＜0}，N={x|x-3≤0}，则M∩N为（ ）
| A、（-∞，-1）∪（2，3] |
| B、（-∞，3] |
| C、（2，3] |
| D、（1，3] |
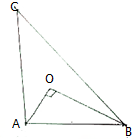如图所示，已知点O为△ABC的重心，OA⊥OB，AB=6，则