题目内容
3.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,长轴长等于4,离心率为$\frac{1}{2}$,直线AB过焦点F1且与椭圆C交于A、B两点(A在第一象限),△F1AF2与△F1BF2的面积比为7:3.(1)求椭圆的方程;
(2)求直线AB的方程.
分析 (1)由于2a=4,$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解出即可得出.
(2)可设直线AB的方程为:my-1=x,A(x1,y1),B(x2,y2).与椭圆方程联立化为:(3m2+4)y2-6my-9=0,由△F1AF2与△F1BF2的面积比为7:3.可得$\frac{{y}_{1}}{-{y}_{2}}$=$\frac{7}{3}$,与根与系数的关系联立解出m即可得出.
解答 解:(1)∵2a=4,$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,解得a=2,c=1,b2=3.
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)可设直线AB的方程为:my-1=x,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{my-1=x}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为:(3m2+4)y2-6my-9=0,
∴y1+y2=$\frac{6m}{3{m}^{2}+4}$,y1y2=$\frac{-9}{3{m}^{2}+4}$,(*)
∵△F1AF2与△F1BF2的面积比为7:3.
∴$\frac{{y}_{1}}{-{y}_{2}}$=$\frac{7}{3}$,
与(*)联立可得:m=$±\frac{4}{3}$.
∴直线BA的方程为:$±\frac{4}{3}$y-1=x,即3x±4y+3=0.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 若l∥α,则α内存在无数条直线与l平行 | |
| B. | 若α⊥β,则α内存在无数条直线与β不垂直 | |
| C. | 若α∥β,则α内存在直线m,β内存在直线,使得m⊥n | |
| D. | 若a⊥l,b⊥l,则a与b不可能垂直 |
| A. | 15 | B. | 5 | C. | -1 | D. | -3 |
| A. | -1 | B. | 1 | C. | 3 | D. | -3 |
| A. | f(x)=|lnx|(x>0) | B. | f(x)=ln|x|(x≠0) | C. | f(x)=x-$\frac{1}{x}$(x≠0) | D. | f(x)=x+$\frac{1}{x}$(x≠0) |
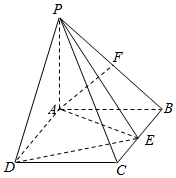 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.