题目内容
13.已知复数z=a+(a-2)i(a∈R,i是虚数单位)为实数,则$\int_0^a{\sqrt{4-{x^2}}dx}$的值是( )| A. | 2+π | B. | $2+\frac{π}{2}$ | C. | π | D. | 4+4π |
分析 首先复数为实数,得到a,然后利用定积分的几何意义求值.
解答 解:因为复数z=a+(a-2)i(a∈R,i是虚数单位)为实数,所以a=2,所以$\int_0^a{\sqrt{4-{x^2}}dx}$=${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx$=$\frac{1}{4}π×4$=π;
故选:C
点评 本题考查了复数的性质以及定积分的计算;比较基础.

练习册系列答案
相关题目
9.双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线方程为( )
| A. | y=±3x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
18.不等式|x|•(1-2x)>0的解集是( )
| A. | $(-∞,\frac{1}{2})$ | B. | (-∞,0)∪$(0,\frac{1}{2})$ | C. | $(\frac{1}{2},+∞)$ | D. | $(0,\frac{1}{2})$ |
5.设集合A={x|x≤$\sqrt{13}$},a=$\sqrt{11}$,那么( )
| A. | a?A | B. | a∉A | C. | {a}∉A | D. | a∈A |
2.设全集U=R,集合A={x∈N|x2<6x},B={x∈N|3<x<8},则如图阴影部分表示的集合是( )
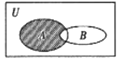

| A. | {1,2,3,4,5} | B. | {1,2,3} | C. | {3,4} | D. | {4,5,6,7} |
3.已知函数$f(x)=\frac{{{e^x}-{e^{-x}}}}{2}$,x1、x2、x3∈R,且x1+x2>0,x2+x3>0,x3+x1>0,则f(x1)+f(x2)+f(x3)的值( )
| A. | 一定等于零 | B. | 一定大于零 | C. | 一定小于零 | D. | 正负都有可能 |
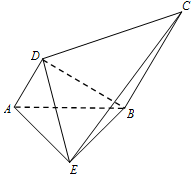 如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,
如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,