题目内容
14.如图是一个空间几何体的三视图,则该几何体的表面三角形中为直角三角形的个数为( )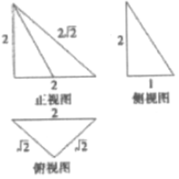
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由三视图可知:该几何体为一个三棱锥P-ABC,其中PC⊥底面ABC,底面ABC是一个三边分别为$\sqrt{2}$,$\sqrt{2}$,2的三角形,PC=2.利用勾股定理的逆定理、线面垂直的判定与性质定理、三垂线定理即可判断出结论.
解答 解:由三视图可知:该几何体为一个三棱锥P-ABC,其中PC⊥底面ABC,底面ABC是一个三边分别为$\sqrt{2}$,$\sqrt{2}$,2的三角形,PC=2.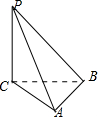
由$(\sqrt{2})^{2}+(\sqrt{2})^{2}={2}^{2}$,可得∠A=90°.
又PC⊥底面ABC,∴PC⊥BC,PC⊥AC.
又三垂线定理可得:AB⊥AC.
因此该几何体的表面三角形中为直角三角形的个数为4.
故选:C.
点评 本题考查了三棱锥的三视图、勾股定理的逆定理、线面垂直的判定与性质定理、三垂线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.在△ABC中,B=30°,AB=$\sqrt{3}$,AC=1,则△ABC的面积是( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ |
6.已知函数$f(x)=\left\{\begin{array}{l}{log_2}({{x^2}+x+a}),x≥1\\ 1-{x^2},x<1\end{array}\right.$的值域为R,则常数a的取值范围是( )
| A. | [0,+∞) | B. | (-2,-1] | C. | (-2,0] | D. | (-∞,0] |
4.已知命题$p:t=\frac{π}{2}$,命题q:${∫}_{0}^{t}$sinxdx=1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
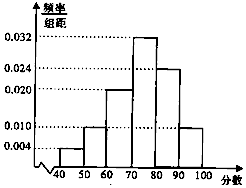 某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.