题目内容
3.求抛物线y2=2x与直线2x+y-2=0围成的平面图形的面积.分析 首先求出两个曲线的几点,利用定积分表示曲边梯形的面积,然后计算定积分.
解答 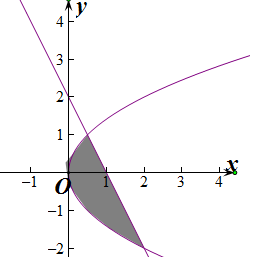 解:方程组$\left\{\begin{array}{l}{{y}^{2}=2x}\\{2x+y-2=0}\end{array}\right.$,解得交点坐标为($\frac{1}{2}$,1),(2,-2),
解:方程组$\left\{\begin{array}{l}{{y}^{2}=2x}\\{2x+y-2=0}\end{array}\right.$,解得交点坐标为($\frac{1}{2}$,1),(2,-2),
所求面积为S=${∫}_{-2}^{1}$(1-$\frac{1}{2}$y-$\frac{1}{2}$y2)dy
=(y-$\frac{1}{4}$y2-$\frac{1}{6}$y3)|${\;}_{-2}^{1}$=(1-$\frac{1}{4}$-$\frac{1}{6}$)-(-2-1+$\frac{4}{3}$)=$\frac{9}{4}$.
点评 本题考查了利用定积分求曲边梯形的面积;关键是利用定积分正确表示.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如图是一个空间几何体的三视图,则该几何体的表面三角形中为直角三角形的个数为( )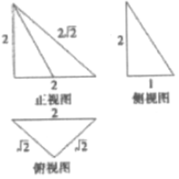

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |