题目内容
7.设ω>0,函数$y=sin(ωx+\frac{π}{3})+4$的图象向右平移$\frac{3π}{4}$个单位后与原图象重合,则ω的最小值是( )| A. | $\frac{3}{8}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{8}{3}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性,可得$\frac{3π}{4}$=k•$\frac{2π}{ω}$,k∈Z,由此求得ω的最小值.
解答 解:把函数$y=sin(ωx+\frac{π}{3})+4$的图象向右平移$\frac{3π}{4}$个单位后,可得y=sin[ω(x-$\frac{3π}{4}$)+$\frac{π}{3}$]+4 的图象,
根据所得图象与原图象重合,可得$\frac{3π}{4}$=k•$\frac{2π}{ω}$,即ω=$\frac{8k}{3}$,k∈Z,
故ω的最小值是$\frac{8}{3}$.
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性,属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.函数$y=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,则( )
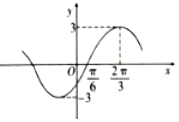

| A. | $y=3sin({2x-\frac{π}{6}})$ | B. | $y=3sin({2x-\frac{π}{3}})$ | C. | $y=3sin({x-\frac{π}{6}})$ | D. | $y=3sin({x-\frac{π}{3}})$ |
2.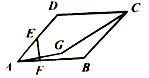 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )| A. | $\sqrt{7}-1$ | B. | 2 | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}$ |
12.在△ABC中,角A,B,C的对边分别为a,b,c,已知a2-b2=bc,sinC=2sinB,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
19.已知复数z=x+yi,满足|z-3-4i|=1,则x2+y2的取值范围是( )
| A. | [4,6] | B. | [5,6] | C. | [25,36] | D. | [16,36] |