题目内容
13.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知c=$\sqrt{3}$,a2+b2-ab=3,(1)求角C的大小;
(2)若sin A=$\frac{1}{2}$,求b边的长.
分析 (1)由已知及余弦定理可求cosC=$\frac{1}{2}$,结合C为三角形内角,利用特殊角的三角函数值可求C的值.
(2)由sinA=$\frac{1}{2}$,可求A的值,利用三角形内角和定理可求B,进而利用正弦定理可求b的值.
解答 (本小题满分10分)
解:(1)∵c2=a2+b2-2abcosC,c=$\sqrt{3}$,
∴a2+b2-2abcosC=3,
又∵a2+b2-ab=3,
∴cosC=$\frac{1}{2}$,
∴C=$\frac{π}{3}$.
(2)∵sinA=$\frac{1}{2}$,C=$\frac{π}{3}$,
∴$A=\frac{π}{6}或\frac{5π}{6}(舍去\frac{5π}{6})$,
∴$B=\frac{π}{2},由\frac{c}{sinC}=\frac{b}{sinB}得b=2$.
点评 本题主要考查了余弦定理,特殊角的三角函数值,三角形内角和定理,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
3.将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
8.已知x、y满足曲线方程x2+$\frac{1}{{y}^{2}}$=2,则x2+y2的取值范围是( )
| A. | [0,+∞) | B. | [2,+∞) | C. | [$\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{5}{2}$) |
2.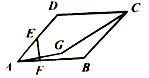 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )| A. | $\sqrt{7}-1$ | B. | 2 | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}$ |